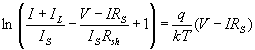![]() 3. Идеальная эффективность преобразования.
3. Идеальная эффективность преобразования.
![]() 4. Солнечный элемент на р-n - структурах.
4. Солнечный элемент на р-n - структурах.
![]() 6.1. Влияние температуры и радиации.
6.1. Влияние температуры и радиации.
![]() 7.2. Солнечные элементы на барьерах Шоттки и МДП - структурах.
7.2. Солнечные элементы на барьерах Шоттки и МДП - структурах.
![]() 3. Идеальная эффективность преобразования.
3. Идеальная эффективность преобразования.
![]() 4. Солнечный элемент на р-n - структурах.
4. Солнечный элемент на р-n - структурах.
![]() 6.1. Влияние температуры и радиации.
6.1. Влияние температуры и радиации.
![]() 7.2. Солнечные элементы на барьерах Шоттки и МДП - структурах.
7.2. Солнечные элементы на барьерах Шоттки и МДП - структурах.
1. ВВЕДЕНИЕ
В настоящее время солнечные батареи являются наиболее важным источником энергии для спутников и космических кораблей при длительных полетах. Они успешно применяются также и на Земле. В связи с увеличением потребления энергии во всем мире запасы обычных источников энергии (различных видов ископаемого топлива) должны истощиться в не слишком отдаленном будущем. Поэтому необходимо разрабатывать и использовать альтернативные источники энергии, и особенно наш единственный практически неистощимый естественный источник энергии — Солнце. Считается, что основным поставщиком солнечной энергии будут солнечные батареи, поскольку они преобразуют солнечный свет непосредственно в электричество с высоким коэффициентом преобразования, создают почти постоянную мощность при низких эксплуатационных расходах и фактически не загрязняют окружающую среду. В последнее время наблюдается расширение исследований и разработок дешевых плоскопанельных, а также тонкопленочных солнечных батарей, систем концентраторов и многих новых идей. Следует ожидать, что в ближайшем будущем стоимость отдельного солнечного элемента и комплектуемых на его основе больших солнечных батарей снизится настолько, что окажется экономически выгодным использование солнечной энергии в больших масштабах.
Первый солнечный элемент был создан Чапеном, Фуллером и Пирсоном в 1954 г. на основе диффузионного кремниевого р—п-перехода. Впоследствии Рейнольдс и др. разработали солнечный элемент на сульфиде кадмия. Затем солнечные элементы были созданы на многих других полупроводниках с использованием различных конструкций прибора и применением монокристаллических и поликристаллических материалов и аморфных тонкопленочных структур. Исчерпывающий анализ основных характеристик солнечных элементов проведен Ховелом. Обзор основных важнейших работ по солнечным батареям за период до 1974 г. составлен Бекусом. Палфри и Джонстон составили обзоры по фотовольтаическим элементам, а в работе Бечмана обсуждаются проблемы выбора материала для солнечных батарей. Результаты последних исследований можно найти в сборниках "конференций для специалистов по фотовольтаическим эффектам".
2. Солнечное излучение.
Источником солнечного излучения служит термоядерная реакция. Каждую секунду примерно 6*1011 кг Н2 превращаются в Не. Дефект массы при этом составляет 4000 кг, что приводит в соответствии с соотношением Эйнштейна Е=mc2 к выделению энергии, равной 4*1020 Дж. Основная часть этой энергии испускается в виде электромагнитного излучения в диапазоне от ультрафиолетового до инфракрасного (0,2-3 мкм). Полная масса Солнца в настоящее время составляет ~2*1030 кг, что должно обеспечить его достаточно стабильное существование примерно с постоянным выделением энергии в течение свыше 10 млрд. лет.
Интенсивность солнечного излучения в свободном пространстве на расстоянии, равном среднему расстоянию между Землей и Солнцем, называется солнечной радиацией. Ее величина равна 1353 Вт/м2. При прохождении через атмосферу солнечный свет ослабляется в основном благодаря поглощению ультрафиолетового излучения озоном и рассеянию излучения находящимися в воздухе частицами пыли и аэрозолями. Показатель атмосферного влияния на интенсивность солнечного излучения, доходящего до земной поверхности, определяется “воздушной массой”. Величина последней равна секансу угла между Солнцем и зенитом.
На рис.1 приведены четыре кривые, иллюстрирующие спектральное распределение интенсивности солнечного излучения (мощность на единицу площади в единичном интервале длин волн). Верхняя кривая соответствует солнечному спектру за пределами земной атмосферы, т.е. при нулевой воздушной массе (АМ0). Это распределение можно аппроксимировать распределением интенсивности черного тела при температуре 5800 К. Спектр АМ0 определяет работу солнечных батарей на спутниках и космических кораблях. Спектр АМ1 соответствует распределению солнечного излучения на поверхности Земли, когда солнце стоит в зените; при этом полная мощность излучения составляет ~925 Вт/м2.
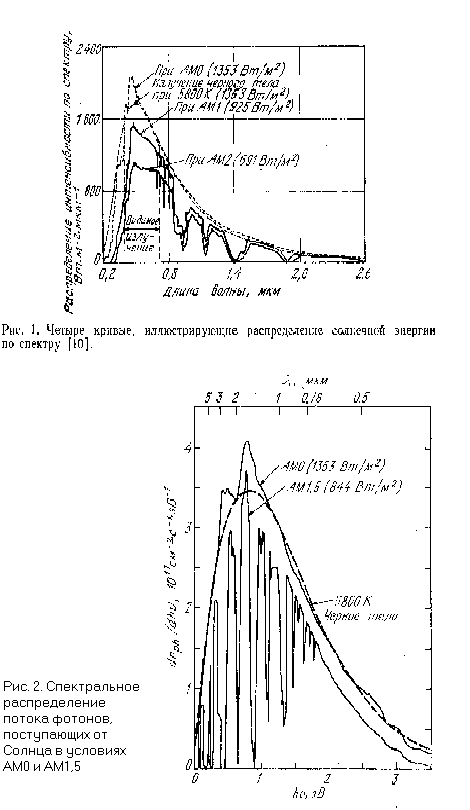
Средняя интенсивность излучения на Земле примерно совпадает с интенсивностью излучения, прошедшего через воздушную массу, равную 1,5, что соответствует положению Солнца под углом 45 к горизонту. На рис.2 приведено распределение числа фотонов, приходящихся на единичный энергетический интервал на 1 см2 за 1 с в условияхАМ0 и АМ1,5. Для перевода длинны волны (мкм) в энергию фотона (эВ) мы использовали соотношение
l = ![]()
Полная мощность солнечного излучения при АМ1,5 составляет 844 Вт/м
2.3. Идеальная эффективность преобразования.
Обычный солнечный элемент (например, p – n-переход) имеет лишь одну характерную энергию – ширину запрещенной зоны Eg. Когда на элемент попадает солнечный свет, фотоны с энергией, меньшей Eg, не дают вклада в выходную мощность элемента (в пренебрежении поглощением света, сопровождаемым возбуждением фотонов). Каждый фотон с энергией, большей Eg, дает вклад, равный Eg, в выходную мощность, а остальная часть энергии фотона переходит в тепло. Для того чтобы определить эффективность ( или идеальный к.п.д.) преобразования, рассмотрим диаграмму энергетических зон освещаемого p –n-перехода (рис.4,а). Будем полагать, что солнечный элемент имеет идеальную вольт-амперную характеристику (ВАХ). Соответствующая эквивалентная цепь показана на рис.4,б , где параллельно переходу введен источник постоянного тока IL, описывающий возбуждение неравновесных носителей солнечным излучением. Ток насыщения диода Is определен, RL – нагрузочное сопротивление.
ВАХ такого прибора определяется выражениями
I=IS(e qV/kT – 1) - IL (2)
и
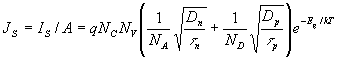 (3)
(3)
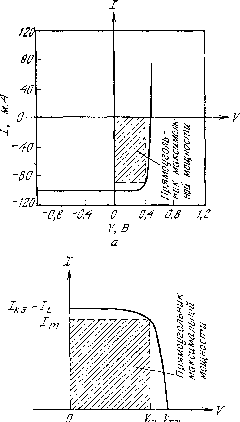
Где А – площадь прибора. График ВАХ, определяемой формулой (2), приведен на рис.5,а для следующих параметров: I
L=100 мА, IS=1 нА, А=4 см2 и Т=300 К. Поскольку ВАХ проходит через четвертый квадрант, это означает, что прибор служит источником энергии. При соотвецтвующем подборе нагрузочного сопротивления вырабатываемая энергия может достигать 80% произведения Iкз Vxx (Iкз – ток короткого замыкания, Vxx – напряжение холостого хода элементов). Чаще ВАХ элемента изображают так, как показано на рис.5,б. На рис.5,б также определены величины Im и Vm – значения тока и напряжения, при которых реализуется максимальная выходная мощность Pm ( Pm = Im Vm ).Из уравнения (2) получаем, что напряжение холостого хода (при I=0) равно
Vxx = ![]()
Следовательно при заданном токе I
L напряжение холостого хода логарифмически возрастает при у меньшении тока насыщения IS. Выходная мощность равнаP = IV = ISV(e![]() - 1) – ILV.
- 1) – ILV.
Условие максимума мощности получаем, положив dP/dV = 0, откуда имеем
Im= IS
bVmeVm = ![]()
где
b=q/kT . Максимальная выходная мощность определяется выражениемPm = ImVm ![]() ,
,
где
Em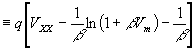 .
.
Величина Еm соответствует той максимальной энергии, которая выделяется в нагрузке при поглощении одного фотона и при оптимальном согласовании элемента с цепью.
Для данного полупроводника плотность тока насыщения J
S может быть получена из формулы (3). Минимальное значение JS для Si при 300 К составляет ~10-15 А/см2. При АМ1,5 плотность тока короткого замыкания JКЗ, равную JL, можно получить графически из рис.2:J
КЗ = JL(Eg) =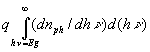 .
.Результат такого интегрирования показан на рис.6 (кривая 1).
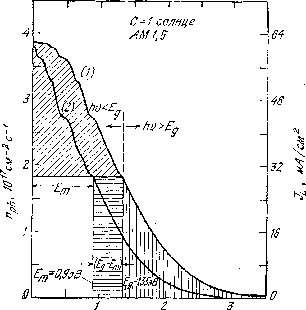
Рис. 6. Зависимость плотности потока фотонов в солнечном спектре от энергии фотона и графический метод определения эффективности преобразования
Если значения J
S и JL известны, величину Еm можно получить с помощью численного решения трансцендентных уравнений (4), (7) и (9). Поскольку величина Em зависит от JS , она зависит также от параметров материала (таких, как t, D и уровня лигирования). Идеальная эффективность преобразования реализуется при оптимальном выборе параметров материала, когда величина JS минимальна. Поведение Em для полупроводников с различной шириной запрещенной зоны показано на рис.6 (кривая г). Идеальная эффективность преобразования равна отношению максимальной выходной мощности к внешней мощности (мощности падающего излучения) Pin и может быть определена графически из рис.6: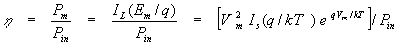
или
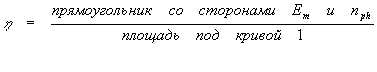
где площадь под кривой 1 равна 5,2*10
17 эВ/(см2*с). Максимальная эффективность оказывается равной 31 % и достигается при Eg=135 эВ, если использовать параметры материала, характерные для полупроводников типа АIIIBV.На рис.7 приведена зависимость идеальной эффективности солнечного элемента при 300 К от ширины запрещенной зоны. Кривая с отметкой С=1 соответствует АВ1,5. Небольшие осцилляторы на ней связаны с характером поглощения излучения в атмосфере. Предельное значение идеальной эффективности можно также вычислить на основании принципа детального равновесия или в предположении, что потери обусловлены лишь излучательной рекомбинацией. Эти методы также приводят к результатам, близким к получаемым с помощью графического построения и приведенным на рис.7. Отметим, что кривая эффективности имеет широкий максимум, в пределах которого к.п.д. слабо зависит от Eg. Поэтому все полупроводники, которые имеют ширину запрещенной зоны от 1 до 2 эВ, относятся к материалам пригодным для создания солнечных элементов. Существует ряд факторов, снижающих идеальную эффективность, вследствие чего реальные значения эффективности преобразования ниже идеальных. О реальных солнечных элементах речь пойдет в следующих разделах.
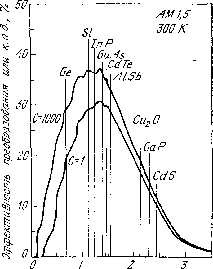
Рис. 7. Зависимость идеального к. п. д. солнечного элемента от Ед при солнечном освещении и при 1000-кратной концентрации солнечного излучения Г = 300 Ю.
На рис.7 приведена также кривая идеальной эффективности для случая оптически сконцентрированного излучения интенсивностью 1000 солнц (т.е. 844 кВт/м2). Максимум идеальной эффективности преобразования возрастает с 31 % (при С=1) до 37 % (при С=1000). Это возрастание связано в основном с увеличением VXX, которое приводит к увеличению Еm в соотвецтвии с формулой (9). Поведение плотности тока короткого замыкания JL иллюстрируется на рис.8. Отметим, что расстояние по горизонтали между кривыми 1 и 2 на этом рисунке меньше чем на рис.6. На рис.8 приведена также зонная диаграмма полупроводниковой структуры, которую можно использовать для высокоэффективного преобразования концентрированного солнечного излучения. Для нахождения максимальной эффективности можно использовать графический метод, положив плотности тока во всех p – n-переходах одинаковыми. Для двух последовательных p – n-переходов максимально возможным к.п.д. достигает 50 % и реализуется при Eg1=156 эВ и Eg2=0,94 эВ. Для трех переходов к.п.д. достигает 56 % при Eg1=1,75 эВ, Eg2=1,18 эВ и Eg3=075 эВ. При дальнейшем увеличении числа переходов к.п.д. растет очень медленно: так, при 36 переходах максимум к.п.д. равен 72 %.
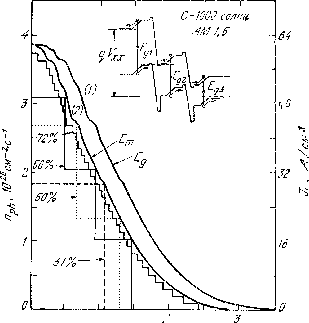 Рис. 8. Зависимость плотности потока фотонов от их энергии в спектре концентрированного солнечного излучения и графический метод определения к. п. д. в каскадных солнечных элементах с последовательно соединенными р — n-переходами
Рис. 8. Зависимость плотности потока фотонов от их энергии в спектре концентрированного солнечного излучения и графический метод определения к. п. д. в каскадных солнечных элементах с последовательно соединенными р — n-переходами
4. Солнечные элементы на p-n – переходах.
В этом разделе рассмотрены прежде всего кремниевые солнечные элементы с p– n-переходами, поскольку они служат как бы эталонным прибором для всех солнечных батарей. жат основным источником питания при длительных полетах. При этом главными проблемами являются эффективность преобразования и надежность элемента, поскольку под влиянием частиц с высокой энергией на внешних орбитах характеристики элемента ухудшаются со временем. В наземных условиях можно применять как плоские солнечные батареи, так и системы солнечных батарей с концентраторами. При этом наряду с проблемами повышения эффективности преобразования и надежности элемента на первом плане оказывается проблема снижения его стоимости, поскольку необходимо, чтобы наземные солнечные системы оказались в конце концов конкурентоспособными с другими источниками энергии.
Работы по наземным плоскопанельным системам направлены в основном на максимально возможное снижение стоимости батарей при одновременном сохранении к. п. д. преобразования на уровне не менее 10 %. Для этой цели используются такие методы создания подложек, как выращивание ленты через фильеру или способом “пластина к пластине” и выращивание дендритных лент. Для снижения стоимости подложек также применяется выращивание поликристаллического кремния на керамике либо на металлургическом кремнии. К наиболее вероятным кандидатам для использования в плоскопанельных системах следует отнести солнечные элементы на аморфном кремнии и на тонких пленках. Работы по созданию концентрирующих систем направлены в основном на увеличение к. п. д. преобразования в условиях высокой концентрации солнечной энергии и на минимизацию стоимости всей системы как целого. В следующем разделе мы проанализируем основные рабочие характеристики солнечных элементов с p - n-переходами.
5. Спектральный отклик.
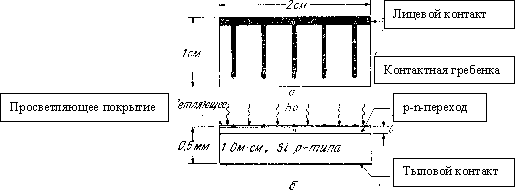
Схематически типичный солнечный элемент изображен на рис. 9. Он состоит из мелкого p - n-перехода, созданного у поверхности (например, с помощью диффузии), лицевого омического полоскового контакта, тылового омического сплошного контакта и просветляющего покрытия на лицевой поверхности.
Если на лицевую поверхность падает монохроматический свет с длиной волны l, фототок и спектральный отклик (число коллектируемых электронов, приходящихся на один падающий фотон с данной длиной волны) можно определить следующим образом. Скорость генерации электронно-дырочных пар на расстоянии x от поверхности полупроводника (рис. 10, а) определяется выражением
![]()
где
a(l) – коэффициент поглощения, F(l) – плотность потока падающих фотонов в единичном спектральном интервале, R(l) – доля фотонов отражающихся от поверхности.При низком уровне инжекции одномерные стационарные уравнения непрерывности имеют вид
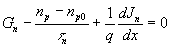 (13)
(13)
для электронов в полупроводнике р-типа и
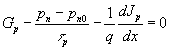 (14)
(14)
для дырок в полупроводнике n-типа. При этом плотность тока электронов и дырок соответственно определяются выражениями
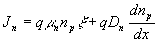 , (15)
, (15)
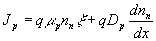 . (16)
. (16)
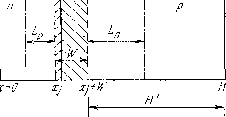
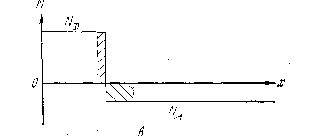
В солнечном элементе с резким p – n-переходом и постоянными уровнями легирования по обеим сторонам перехода (рисю10, б и в) вне обедненной области электрическое поле отсутствует. Если рассматривается переход с подложкой р-типа и n-слоем у лицевой поверхности, с помощью уравнений (12), (14) и (16)
Можно получить уравнение описывающее распределение неосновных носителей в верхней части перехода:
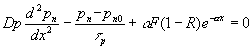 . (17)
. (17)

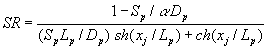
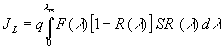
где
lm – красная граница поглощения, определяемая шириной запрещенной зоны полупроводника.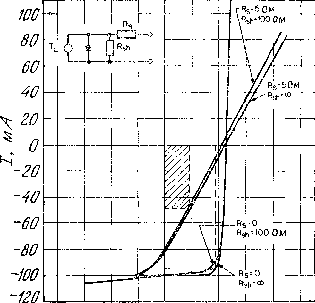
Рис. 12. Теоретические вольтамперные характеристики солнечного элемента при различных значениях последовательного и параллельного сопротивлений. На вставке показана эквивалентная схема. Параметры элемента те же, что использовались на рис. 5