Глава 2.10
Как уже отмечалось в разделе 2.8, для получения в явном виде вольтамперной характеристики транзистора необходимо найти связь между поверхностным потенциалом ![]() и квазиуровнем Ферми
и квазиуровнем Ферми ![]() . Рассмотрим для этого уравнение электронейтральности
. Рассмотрим для этого уравнение электронейтральности
| (2.10.1) |
Заряд в ОПЗ состоит из заряда свободных электронов Qn в канале и заряда ионизованных акцепторов QВ, так показано в (2.9.7). Разложим заряд QВ по степеням ![]() вблизи порогового значения поверхностного потенциала
вблизи порогового значения поверхностного потенциала ![]() .
Имеем
.
Имеем
| (2.10.2) |
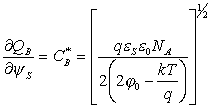 . . |
(2.10.3) |
Величина C*B - емкость обедненной области при пороговом значении поверхностного потенциала ![]() ,
, ![]() .
.
С учетом (2.10.2) и (2.10.3) соотношение (2.10.1) примет вид
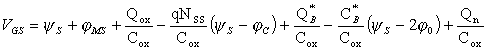 . . |
(2.10.4) |
Назовем пороговым напряжением VТ напряжение на затворе МДП-транзистора VGS в равновесных условиях ( ![]() ) соответствующее пороговому потенциалу
) соответствующее пороговому потенциалу ![]() .
.
| (2.10.5) |
Из (2.10.4) и (2.10.5) следует, что
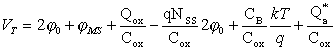 . . |
(2.10.6) |
С учетом написанного для порогового напряжения соотношения (2.10.6) уравнение электронейтральности примет вид
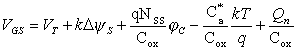 , , |
(2.10.7) |
где n и ![]() будут
будут
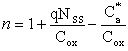 ; ; |
Слагаемое ![]() в уравнении (2.10.7) соответствует заряду свободных электронов Qn при пороговом значении поверхностного потенциала и обычно мало по сравнению с остальными слагаемыми, входящими в правую часть уравнения (2.10.7).
в уравнении (2.10.7) соответствует заряду свободных электронов Qn при пороговом значении поверхностного потенциала и обычно мало по сравнению с остальными слагаемыми, входящими в правую часть уравнения (2.10.7).
Для области слабой инверсии заряд свободных электронов мал и последним слагаемым в (2.10.7) можно пренебречь. Поскольку напряжение на затворе VGS и пороговое напряжение VТ постоянные величины, то из (2.10.7) следует, что для области слабой инверсии в каждой точке инверсионного канала величина ![]() должна оставаться постоянной. Постоянную величину найдем из того условия, что вблизи истока
должна оставаться постоянной. Постоянную величину найдем из того условия, что вблизи истока ![]() = 0 и, следовательно
= 0 и, следовательно
| (2.10.8) |
Отсюда следует, что в предпороговой области зависимость поверхностного потенциала ![]() от квазиуровня Ферми
от квазиуровня Ферми ![]() будет определяться следующим выражением
будет определяться следующим выражением
| (2.10.9) |
Здесь ![]() - значение поверхностного потенциала в точке канала, где
- значение поверхностного потенциала в точке канала, где ![]() = 0 .
Величина m равна
= 0 .
Величина m равна
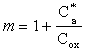 . . |
(2.10.10) |
Таким образом, в МДП-транзисторе в области слабой инверсии при отсутствии захвата на поверхностные состояния ( Nss = 0 ; m = n ) поверхностный потенциал ![]() не зависит от квазиуровня Ферми
не зависит от квазиуровня Ферми ![]() и следовательно постоянен вдоль инверсионного канала. Этот важный вывод обуславливает целый ряд особенностей в характеристиках МДП транзистора в области слабой инверсии.
и следовательно постоянен вдоль инверсионного канала. Этот важный вывод обуславливает целый ряд особенностей в характеристиках МДП транзистора в области слабой инверсии.
Для области сильной инверсии при ![]() в уравнении (2.10.7) в правой части доминирует слагаемое, связанное со свободными носителями заряда QW . Поэтому требуется, чтобы вдоль канала в каждой точке величина заряда электронов Qn оставалась постоянной. Поскольку в этой области для Qn справедливо выражение (2.9.11), получаем
в уравнении (2.10.7) в правой части доминирует слагаемое, связанное со свободными носителями заряда QW . Поэтому требуется, чтобы вдоль канала в каждой точке величина заряда электронов Qn оставалась постоянной. Поскольку в этой области для Qn справедливо выражение (2.9.11), получаем
Следовательно в области сильной инверсии
| (2.10.11) |
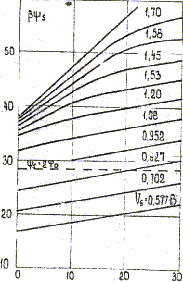
Рис. 2.10.1.Зависимость поверхностного потенциала ![]() от величины квазиуровня Ферми
от величины квазиуровня Ферми ![]() в канале МОП ПТ при различных напряжениях затвора VG , B.
в канале МОП ПТ при различных напряжениях затвора VG , B.
VT = 0,95 В ; Nss = 1012см-2эВ-1 ; NA = 1016см-3 ; dox = 50A .
Пунктирная линия соответствует условию ![]() .
.
На рис.2.10.1 в качестве примера приведен расчет функциональной связи между ![]() и
и ![]() по уравнению (2.10.7), выполненный численным методом. Параметры для расчета указаны в подписи к рисунку.
по уравнению (2.10.7), выполненный численным методом. Параметры для расчета указаны в подписи к рисунку.
Зная связь между поверхностным потенциалом ![]() и величиной квазиуровня Ферми
и величиной квазиуровня Ферми ![]() можно получить соотношение между дрейфовой и диффузионной составляющей тока в произвольной точке канала. Действительно, из (2.8.8, 2.8.9) и (2.10.9) следует, что для области слабой инверсии
можно получить соотношение между дрейфовой и диффузионной составляющей тока в произвольной точке канала. Действительно, из (2.8.8, 2.8.9) и (2.10.9) следует, что для области слабой инверсии
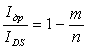 . . |
(2.10.12) |
В области слабой инверсии при отсутствии захвата ( NSS = 0, m = n ) весь ток канала диффузионный. При наличии захвата на поверхностные состояния появляется дрейфовая составляющая. Физически она обусловлена появлением продольного электрического поля за счет различия в заполнении поверхностных состояний вдоль канала. При заполнении поверхностных состояний основными носителями тока инверсионного канала дрейфовый и диффузионный ток имеют одно и то же направление. При условии постоянства плотности поверхностных состояний NSS ( ![]() ) в запрещенной зоне полупроводника соотношение между диффузионной и дрейфовой составляющей в области слабой инверсии сохраняется.
) в запрещенной зоне полупроводника соотношение между диффузионной и дрейфовой составляющей в области слабой инверсии сохраняется.
Для области сильной инверсии из (2.8.8, 2.8.9) и (2.10.11) следует, что диффузионный ток равен нулю и весь ток канала дрейфовый
| (2.10.13) |
В области перехода от слабой к сильной инверсии доля дрейфовой составляющей в полном токе канала возрастает от значения, определяемого соотношением (2.10.12), до единицы.
| Глава 2.9 | Содержание | Глава 2.11 |