4.2. Закон Гука для анизотропных твердых тел и энергия упругодеформированного тела
Монокристаллы являются в общем случае анизотропными телами, т. е. любые
произвольно выбранные направления в монокристалле не эквивалентны. Выше было
показано, что однородные напряжение и деформация описываются тензорами второго
ранга, каждый из которых определяется девятью компонентами деформации ![]() и напряжений
и напряжений ![]() .
.
Если деформация бесконечно мала и однородна, то каждая компонента тензора деформации линейно связана со всеми компонентами тензора напряжений, и наоборот [59]. Эта связь выражается законом Гука для анизотропных твердых тел. Математическая запись закона Гука для монокристаллов:
|
|
(4.25) |
Справедлив и обратный закон
|
|
(4.26) |
В формулах
(4.25) и (4.26) ![]() – постоянная упругой податливости, а
– постоянная упругой податливости, а ![]() – постоянная упругой жесткости.
– постоянная упругой жесткости.
В развернутом виде уравнения (4.25) и (4.26) представляются девятью
уравнениями с 81 коэффициентами S и C. Совокупность ![]() (
(![]() )
образует тензор четвертого ранга. Поскольку тензоры деформаций и напряжений –
симметричные тензоры второго ранга (т. е.
)
образует тензор четвертого ранга. Поскольку тензоры деформаций и напряжений –
симметричные тензоры второго ранга (т. е. ![]() ;
; ![]() ), то независимых компонент в S и C будет не 81, а
только 36.
), то независимых компонент в S и C будет не 81, а
только 36.
|
|
(4.27) |
Кроме того, тензоры S и C симметричны и относительно перестановки пар индексов
|
|
(4.28) |
Это приводит к тому, что в общем случае число независимых компонент
сокращается с 36 до 21. Именно 21 упругую константу имеет твердое тело, не
обладающее никакой симметрией. Для сокращения числа индексов вводят так
называемые матричные обозначения, согласно которым пары индексов заменяются
однократными (замена показана символом ®).
![]() . Исходя из этих обозначений, можно произвести замену
индексов в тензоре напряжений
. Исходя из этих обозначений, можно произвести замену
индексов в тензоре напряжений
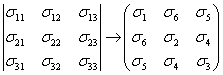
и в тензоре деформаций
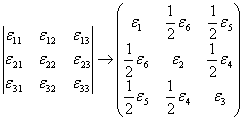
Тогда закон Гука будет иметь вид
|
|
(4.29) |
т. к. 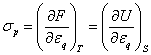 .
.
Дифференцируя по ![]() , имеем
, имеем
|
|
(4.30) |
Аналогично ![]() .
.
Наличие симметрии кристалла также накладывает определенные условия на
компоненты тензора модулей упругости ![]() ,
в результате чего их становится меньше, чем 21.
,
в результате чего их становится меньше, чем 21.
Рассмотрим частный случай кубического кристалла.
1. Симметрия куба обуславливает одинаковость характеристик кубических кристаллов вдоль осей координат
![]() .
.
2. Вдоль пространственных диагоналей направлены оси симметрии третьего порядка, т. е.
![]() ;
;
и
![]() .
.
3. Вращательные компоненты сил не могут привести к растяжению куба, поэтому
![]() .
.
4. Силы, действующие на площадку перпендикулярную оси z, не могут изменить угол между осями z и x, т. е.
![]() .
.
Следовательно, для кубической системы имеем следующую связь между компонентами тензоров напряжений и деформации.
|
|
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
|
s1 |
С11 |
С12 |
С12 |
0 |
0 |
0 |
|
s2 |
С12 |
С11 |
С12 |
0 |
0 |
0 |
|
s3 |
С12 |
С12 |
С11 |
0 |
0 |
0 |
|
s4 |
0 |
0 |
0 |
С44 |
0 |
0 |
|
s5 |
0 |
0 |
0 |
0 |
С44 |
0 |
|
s6 |
0 |
0 |
0 |
0 |
0 |
С44 |
Таким образом, в кубической системе остается только три независимых модуля упругости и столько же постоянных упругой податливости.
Связь между ![]() и
и ![]() для кубического
кристалла
для кубического
кристалла
Матрицы ![]() и
и ![]() взаимосвязаны, т. к. связывают компоненты
тензора напряжений и деформаций
взаимосвязаны, т. к. связывают компоненты
тензора напряжений и деформаций
|
|
(4.31) |
Таким образом, ![]() ,
, ![]() – дельта функция.
– дельта функция.
Поэтому ![]() -
матрица, обратная матрице
-
матрица, обратная матрице ![]() , и наоборот. Если построить матрицу, обратную
, и наоборот. Если построить матрицу, обратную ![]() ,
то для кубических кристаллов получим следующие соотношения:
,
то для кубических кристаллов получим следующие соотношения:
|
|
(4.32) |
Энергия
упругодеформированного тела и объемный модуль упругости
Было показано, что изменение энергии при деформации имеет вид:
|
|
(4.33) |
а компоненты тензора напряжений определяются из формулы
|
|
(4.34) |
Подставим выражение (4.34) в (4.33). Тогда получим
|
|
(4.35) |
В сокращенной форме выражение (4.35) будет иметь вид
|
|
(4.36) |
Интегрируя
уравнение (4.36) и учитывая, что ![]() , получим
, получим
|
|
(4.37) |
В частности, для кубических кристаллов, с учетом вида тензора деформаций ε, имеем
|
|
(4.38) |
Для
однородного всестороннего растяжения ![]() ;
; ![]() , тогда
, тогда
|
|
(4.39) |
Здесь В – объемный модуль упругости, связывающий энергию упругой деформации и квадрат деформации.
|
|
(4.40) |
Экспериментальные данные о коэффициентах упругой жесткости и упругой
податливости для некоторых кристаллов приведены в табл. 4.1 [59, 78]. Коэффициенты упругой жесткости ![]() даны в единицах
даны в единицах ![]() , а упругой податливости
, а упругой податливости ![]() − в
− в ![]() .
.
Таблица 4.1
Коэффициенты
упругой жесткости и упругой податливости (![]() и
и ![]() ) для некоторых кристаллов
) для некоторых кристаллов
Кубическая сингония
|
Вещество |
|
|
|
|
|
|
|
Алмаз |
103,6 |
12,5 |
57,6 |
0,95 |
-0,1 |
1,74 |
|
Ge |
12,89 |
4,83 |
6,71 |
|
|
|
|
Si |
16,74 |
6,52 |
7,96 |
|
|
|
|
GaAs |
11,88 |
5,38 |
5,94 |
11,72 |
-3,65 |
16,83 |
|
ZnS |
10,79 |
7,22 |
4,12 |
18,39 |
-7,07 |
21,69 |
|
KCl |
4,03 |
0,66 |
0,62 |
26,2 |
-3,5 |
160 |
|
LiF |
11,12 |
4,20 |
6,28 |
11,35 |
-3,1 |
15,9 |
|
NaCl |
4,96 |
1,24 |
1,29 |
22,9 |
-4,6 |
79,4 |
|
a-Fe |
24,2 |
14,65 |
11,2 |
|
|
|
|
Na |
0,603 |
0,459 |
0.586 |
6,03 |
-4,59 |
5,86 |
|
Al |
10,73 |
6,09 |
2,83 |
15,7 |
-5,7 |
3,51 |
|
Cu |
16,84 |
12,14 |
7,54 |
14,98 |
-6,29 |
13,26 |
|
W |
51,26 |
20,58 |
15,27 |
|
|
|
Гексагональная сингония
|
Вещество |
|
|
|
|
|
|
Mg |
5,65 |
5,87 |
1,68 |
2,32 |
1,81 |
|
Zn |
15,9 |
6,21 |
4,00 |
3,23 |
4,82 |
|
CdS |
8,16 |
8,08 |
1,43 |
4,95 |
4,79 |
|
b-Кварц |
11,66 |
11,04 |
3,61 |
1,67 |
3,28 |
|
Вещество |
|
|
|
|
|
|
CdS |
20,69 |
16,97 |
-9,99 |
-5,81 |
66,49 |
|
b-Кварц |
9,26 |
10,85 |
-0,80 |
-2,52 |
27,89 |
Тетрагональная сингония
|
Вещество |
|
|
|
|
|
|
|
BaTiO3 |
27,51 |
16,49 |
5,43 |
11,31 |
17,90 |
15,16 |
|
Рутил |
27,3 |
48,4 |
12,5 |
19,4 |
17,6 |
14,9 |
|
Вещество |
|
|
|
|
|
|
|
BaTiO3 |
8,05 |
15,7 |
-2,35 |
-5,24 |
18,4 |
8,84 |
Тригональная сингония
|
Вещество |
|
|
|
|
|
|
|
Кальцит |
13,8 |
7,92 |
3,42 |
4,55 |
4,49 |
-2,07 |
|
a-Кварц |
8,68 |
10,59 |
5,83 |
0,71 |
1,19 |
-1,81 |
|
Корунд |
49,7 |
49,8 |
14,7 |
16,4 |
11,1 |
-2,4 |
|
Теллур |
3,59 |
7,64 |
3,41 |
0,90 |
2,75 |
1,37 |
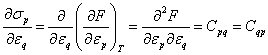 .
.