2.3.1. Ионная связь

В ионных кристаллах электроны переходят от атомов одного типа к атомам другого, так что кристалл состоит из положительных и отрицательных ионов. Для того чтобы с помощью сил электростатического притяжения между валентными электронами и ионными остовами образовать из атомов твердые тела, необходимо выполнить следующие четыре условия [63]:

1.      Положительно заряженные ионные остовы должны находиться на таком расстоянии друг от друга, чтобы при этом было сведено до минимума кулоновское отталкивание между ними.

2.      Валентные электроны должны находиться на определенных расстояниях друг от друга, отвечающих тому же требованию.

3.      Одновременно со вторым условием валентные электроны должны быть настолько близко расположены от положительных ионов, чтобы кулоновское притяжение между разноименными зарядами было максимально.

4.      При выполнении всех этих условий потенциальная энергия системы может уменьшиться, однако это должно происходить таким образом, чтобы кинетическая энергия системы лишь немного возросла.

В ионных кристаллах ионы располагаются так, что кулоновское притяжение между разноименно заряженными ионами сильнее, чем кулоновское отталкивание между ионами одного знака заряда. Таким образом, ионная связь – это связь, обусловленная в основном электростатическим взаимодействием противоположно заряженных ионов [74].

Наиболее характерные ионные кристаллы – NaCl, CsCl (галогениды щелочных металлов).

Как было указано выше, тип связи между атомами во многом определяется степенью ионизации в соединении. Степень ионизации атомов, составляющих ионный кристалл, часто такова, что электронные оболочки всех ионов соответствуют электронным оболочкам, характерным для атомов инертных газов. Например, нейтральные атомы лития и фтора имеют следующую структуру электронной оболочки Li − 1s²2s, F − 1s²2s²2p⁵. В кристалле фтористого лития электронная конфигурация у однократно заряженных ионов становится: Li⁺ − 1s², F^- − 1s²2s²2p⁶. Такая конфигурация характерна для атомов гелия и неона. Атомы инертных газов имеют замкнутые электронные оболочки, и распределение заряда в них имеет сферическую симметрию. Поэтому можно ожидать, что распределение заряда каждого иона в ионном кристалле приближенно обладает сферической симметрией, которая несколько нарушается в области соприкосновения соседних атомов.

На больших расстояниях взаимодействие между ионами с зарядами +q и -q  представляет собой кулоновское притяжение зарядов противоположного знака и кулоновское отталкивание ионов одного знака с потенциалом . При образовании устойчивой кристаллической структуры основной вклад в энергию связи дает электростатическая энергия, которую называют энергией Маделунга. Энергию взаимодействия i-й частицы со всеми остальными частицами, составляющими кристалл, можно рассчитать по формуле (2.13). Предположим, что  в формуле (2.13) может быть представлено в виде суммы двух потенциалов: потенциала сил отталкивания некоторого центрального поля, изменяющегося по закону Борна−Майера (2.9), и кулоновского потенциала . Тогда

.

(2.15)

В формуле (2.15) знак (+) используется в случае одинаковых по знаку зарядов, а знак (–) соответствует разноименным зарядам.

Введем величину , определяемую соотношением , где R – расстояние между соседними ионами в кристалле. Если мы будем учитывать отталкивание только ближайших соседей, то получим

	для ближайших соседей	(2.16)
	для прочих пар атомов.

Таким образом, согласно равенству (2.14), полная энергия:

,

(2.17)

где Z – число ближайших соседей какого-либо иона, N – число ионных пар, а через a обозначена постоянная Маделунга

.

(2.18)

Формулу (2.18) можно переписать в виде:

,

(2.19)

где  – расстояние иона с номером j от исходного.

Полную энергию кристаллической решетки, состоящей из 2N ионов и находящейся в состоянии равновесия, учитывая, что , можно записать в виде:

,

(2.20)

где  – равновесное расстояние между ионами. Выражение (2.20) называется формулой Борна−Майера.

Величина  − энергия Маделунга. Постоянная r имеет размерность длины и приблизительно равна .

Покажем пример расчета постоянной Маделунга на бесконечной цепочке ионов противоположных знаков. Выберем отрицательный заряд как начальный. Обозначим R – расстояние между ионами, тогда

 или иначе .

Множитель 2 перед скобками появляется из-за соседства ионов одного знака слева и справа от исходного. Применим разложение в ряд , тогда x=1 и указанный ряд для a сходится к значению .

Наряду с формулой Борна−Майера (2.20), для расчета энергии сцепления ионного кристалла часто используется формула Борна−Ланде:

.

(2.21)

Здесь  и  − заряды взаимодействующих ионов, n − постоянная, представляющая собой показатель степени в формуле (2.8),  − равновесное расстояние между ионами.

Если известны заряды ионов и структура кристалла (из них можно рассчитать постоянную Маделунга), то для вычисления энергии сцепления нужно знать еще показатель степени в потенциале сил отталкивания n. Его обычно определяют из сжимаемости кристалла æ. По определению,

,

(2.22)

где V − объем кристалла, p − давление. При температуре 0K  , т. е.

.

(2.23)

Объем кристалла можно определить из соотношения  , где N − число пар ионов, g − множитель, значение которого зависит от типа структуры. Так, для структуры NaCl объем, занимаемый  N молекулами, равен , где  − расстояние между ближайшими ионами ( − радиус аниона,  − радиус катиона), . Для CsCl множитель ; для ZnS со структурой вюрцита  и т. д. Используя приближение Борна-Ланде, получим

.

(2.24)

Множитель  появился при записи кулоновского потенциала притяжения в виде  в системе СИ: .

Подставляя в (2.24) , , , м, Кл,  для NaCl, получим  и полную потенциальную энергию, приходящуюся на пару ионов, . Это значение хорошо согласуется с полученным экспериментально при комнатной температуре, которое составило  [63].

Формула Борна−Ланде не является чисто теоретической, т. к. величины n, необходимые для расчета, определяются из экспериментально найденной величины сжимаемости. При этом расхождение теоретических и расчетных данных может доходить до 3 %.

Оценим, пользуясь формулой Борна−Майера (2.20), величину r, имеющую физический смысл размера области, где проявляется взаимодействие отталкивания.

.

(2.25)

Если в формулу (2.25) подставить данные для кристалла NaCl, то получим . Отсюда следует, что взаимодействие отталкивания проявляется в области размером м.
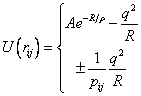
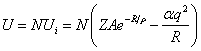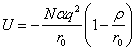