2.2. Энергия связи
Энергию связи системы каких-либо частиц можно интерпретировать как энергию, равную работе, которую необходимо затратить, чтобы разделить эту систему на составляющие ее частицы и удалить их друг от друга на такое расстояние, на котором их взаимодействием можно пренебречь. Проблема связи атомов, составляющих твердое тело, сродни проблеме связи атомов, составляющих молекулу, поэтому для понимания этого вопроса полезно рассмотреть его в контексте межатомной связи в двухатомной молекуле [47].
Пусть
молекула состоит из атомов двух сортов − A и B [68, 74]. Если атомы находятся далеко
друг от друга, то они ведут себя как свободные, не взаимодействуя, пока
расстояние между их центрами много больше суммы радиусов атомов ![]() , где
, где ![]() и
и ![]() – радиусы атомов. Если
при сближении атомов энергия понижается по сравнению с полной энергией двух
изолированных атомов, то между ними возникает сила притяжения. Этому соответствует
уменьшение потенциальной энергии системы
– радиусы атомов. Если
при сближении атомов энергия понижается по сравнению с полной энергией двух
изолированных атомов, то между ними возникает сила притяжения. Этому соответствует
уменьшение потенциальной энергии системы ![]() . При некотором расстоянии
. При некотором расстоянии ![]() энергия
энергия
![]() достигает
минимума. Значению минимума энергии соответствует условие
достигает
минимума. Значению минимума энергии соответствует условие
|
|
(2.2) |
где F − результирующая сила взаимодействия атомов.
Существование минимума
энергии − необходимое условие образования молекулы. При дальнейшем
сближении атомов между ними начинают действовать силы отталкивания, и
потенциальная энергия их взаимодействия возрастает. Полная энергия системы ![]() может быть описана
как сумма двух энергий: энергии притяжения
может быть описана
как сумма двух энергий: энергии притяжения ![]() , имеющей отрицательные значения, и положительной энергии
отталкивания
, имеющей отрицательные значения, и положительной энергии
отталкивания ![]()
|
|
(2.3) |
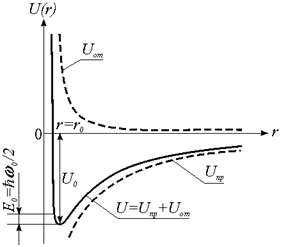
На рис. 2.2 схематически
показаны зависимости потенциальных
энергий притяжения и отталкивания, а также суммарная кривая, соответствующая
полной потенциальной энергии взаимодействия. При некотором расстоянии между
атомами ![]()
![]() , т. е. силы притяжения и отталкивания уравновешиваются, и
образуется молекула AB с наиболее
стабильной конфигурацией. На рис. 2.3 представлена зависимость сил притяжения и
отталкивания между атомами натрия и хлора при образовании молекулы NaCl.
, т. е. силы притяжения и отталкивания уравновешиваются, и
образуется молекула AB с наиболее
стабильной конфигурацией. На рис. 2.3 представлена зависимость сил притяжения и
отталкивания между атомами натрия и хлора при образовании молекулы NaCl.
|
|
|
Рис. 2.2. Зависимость полной потенциальной энергии связи двух атомов
от расстояния между ними |
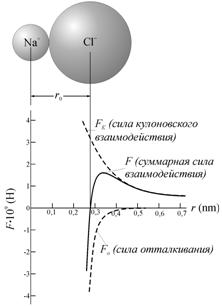
Видно, что при сближении
ионов до некоторого расстояния между центрами атомов основной вклад в суммарную
силу взаимодействия вносит сила притяжения. При расстоянии около 0,33 нм
результирующая сила достигает максимума, после чего уменьшается за счет резкого
роста модуля силы отталкивания. На расстоянии ![]() =0,28 нм равнодействующая сил обращается в нуль. На
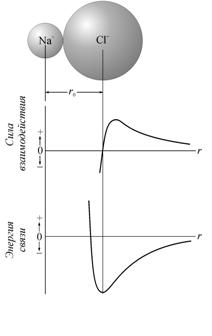
рис. 2.4 приведены кривые силы взаимодействия
и потенциальной энергии для ионов
=0,28 нм равнодействующая сил обращается в нуль. На
рис. 2.4 приведены кривые силы взаимодействия
и потенциальной энергии для ионов
![]() и
и ![]() . В точке обращения силы в нуль потенциальная энергия
взаимодействия достигает минимума.
. В точке обращения силы в нуль потенциальная энергия
взаимодействия достигает минимума.
|
|
|
|
Рис. 2.3. Зависимость
силы взаимодействия ионов Na+—Cl–, показывающая равновесное
состояние, соответствующее длине связи r0 = 0,28 нм [31] |
Рис. 2.4. Сравнение зависимости силы взаимодействия и зависимости
энергии связи ионов Na+—Cl– [31] |
Разложим полную энергию
взаимодействия ![]() в ряд Тейлора в
окрестности точки
в ряд Тейлора в
окрестности точки ![]() .
.
|
|
(2.4) |
Согласно
формуле (2.2) второе слагаемое в разложении (2.4) равно нулю. При малых
значениях ![]() четвертым слагаемым и
слагаемыми более высоких степеней
четвертым слагаемым и
слагаемыми более высоких степеней ![]() можно пренебречь.
Тогда
можно пренебречь.
Тогда
|
|
(2.5) |
представляет
собой параболическую функцию разности ![]() . Действительно, на рис. 2.2 видно, что в непосредственной
близости к точке
. Действительно, на рис. 2.2 видно, что в непосредственной
близости к точке ![]() (
(![]() ) функция U(r) ведет
себя как парабола.
) функция U(r) ведет
себя как парабола.
После образования стабильной
молекулы атомы не находятся в покое, а совершают тепловые колебания около своих
равновесных положений. Из формулы (2.5) следует, что при малых отклонениях от
положения равновесия возвращающая сила пропорциональна расстоянию. Это
соответствует случаю гармонического осциллятора. Уровни энергии осциллятора,
совершающего колебания с собственной частотой ![]() , можно определить из равенства
, можно определить из равенства
|
|
(2.6) |
где n = 0, 1, 2, 3…
Глубина минимума ![]() равна энергии связи
атомов в молекуле (энергия энергетического
сцепления). С учетом энергии нулевых колебаний атомов
равна энергии связи
атомов в молекуле (энергия энергетического
сцепления). С учетом энергии нулевых колебаний атомов ![]() (n = 0) при абсолютном нуле температур энергия связи для
молекулы
(n = 0) при абсолютном нуле температур энергия связи для
молекулы ![]() (см. рис. 2.2).
(см. рис. 2.2).
Для нахождения энергии связи
необходимо знать вид зависимости потенциалов притяжения ![]() и отталкивания
и отталкивания ![]() от расстояния между
взаимодействующими атомами.
от расстояния между
взаимодействующими атомами.
Потенциал притяжения, исходя из его электростатического характера, можно представить степенной функцией
|
|
(2.7) |
где a – положительная постоянная, m – показатель степени.
Потенциал отталкивания обусловлен взаимодействием ядер атомов и зависит от экранировки ядер окружающими его электронами.
|
|
(2.8) |
где b и n − положительные постоянные.
При выводе формулы (2.7) Борном и Ланде была выбрана статическая модель атома, в которой электроны в 8-электронной оболочке размещены по вершинам куба. Квантовомеханический расчет приводит к экспоненциальному выражению для потенциала отталкивания, называемому потенциалом Борна−Майера:
|
|
(2.9) |
где A и r − постоянные величины, определяемые эмпирически.
Учитывая вид потенциальной энергии притяжения Борна−Ланде (2.7) и энергии отталкивания (2.8), потенциальную энергию системы двух атомов можно записать в виде
|
|
(2.10) |
Чтобы функция U(r)
имела минимум, необходимо, чтобы показатель степени потенциала отталкивания был
больше показателя степени потенциала притяжения, т. е. чтобы выполнялось
условие ![]() . Из условия минимума энергии
. Из условия минимума энергии ![]() найдем
равновесное состояние между атомами
найдем
равновесное состояние между атомами ![]() :
:
|
|
(2.11) |
Подставив его в формулу (2.10) для ![]() , получим
, получим
|
|
(2.12) |
Поскольку ![]() , то из формулы (2.12) следует, что энергетическое сцепление
в основном определяется потенциалом сил притяжения.
, то из формулы (2.12) следует, что энергетическое сцепление
в основном определяется потенциалом сил притяжения.
Таким образом, величина энергии связи определяется:
· притяжением атомов, обусловленным взаимодействием валентных электронов;
· кулоновским отталкиванием внутренних оболочек и ядер.
Для устойчивого равновесия необходимо наличие минимума энергии. Существование стабильных связей между атомами в твердом теле предполагает, что полная внутренняя энергия тела, представляющая собой сумму кинетической и потенциальной энергий составляющих его частиц, меньше полной энергии такого же количества свободных атомов. Разность этих двух энергий называется энергией связи.
Если предположить, что энергия взаимодействия двух частиц системы не зависит от присутствия других частиц, то для кристалла в определенной конфигурации энергетические состояния эквивалентных частиц одинаковы, за исключением частиц, находящихся на поверхности. Исходя из этого упрощенного предположения, можно определить энергию взаимодействия любой частицы со всеми остальными.
Пусть ![]() − потенциальная
энергия взаимодействия двух частиц в кристалле, состоящем из N частиц. Выбрав в объеме кристалла центр i-й частицы за начало отсчета,
просуммировав по всем
− потенциальная
энергия взаимодействия двух частиц в кристалле, состоящем из N частиц. Выбрав в объеме кристалла центр i-й частицы за начало отсчета,
просуммировав по всем ![]() , можно найти энергию
, можно найти энергию ![]() взаимодействия i-й частицы со всеми другими
взаимодействия i-й частицы со всеми другими
|
|
(2.13) |
Аналогичное
суммирование можно провести для всех оставшихся ![]() частиц. Тогда полная энергия
решетки из N частиц
частиц. Тогда полная энергия
решетки из N частиц
|
|
(2.14) |
Здесь предполагается, что число частиц N достаточно велико, чтобы можно было пренебречь поверхностными эффектами. Множитель ½ в формуле (2.14) связан с тем, что при суммировании производится учет энергии взаимодействия каждой пары частиц дважды.
В табл. 2.3 [63] представлены значения энергии связи, необходимой для разделения твердого тела на отдельные нейтральные атомы, для большинства химических элементов. Видно, что имеет место существенное отличие в значениях энергии связи для разных столбцов таблицы. Кристаллы инертных газов (правая часть таблицы) имеют малые энергии связи, составляющие несколько процентов и менее от энергии связи для кристаллов элементов, находящихся в столбце C, Si, Ge ... Кристаллы щелочных металлов (левая часть таблицы) имеют промежуточные значения энергии связи, а кристаллы переходных металлов (средние столбцы таблицы) имеют очень большие энергии связи.
Таблица 2.3
Значения энергий
химической связи для некоторых элементов, эВ/ат
|
H 4,48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
He |
|
Li 1,65 |
Be 3,33 |
|
|
|
|
|
|
|
|
|
|
B 5,81 |
C 7,36 |
N − |
O − |
F − |
Ne 0,02 |
|
Na 1,13 |
Mg 1,53 |
|
|
|
|
|
|
|
|
|
|
Al 3,34 |
Si 4,64 |
P − |
S 2,86 |
Cl |
Ar 0,08 |
|
K 0,941 |
Ca 1,825 |
Sc 3,93 |
Ti 4,855 |
V 5,30 |
Cr 4,10 |
Mn 2,98 |
Fe 2,29 |
Co 4,387 |
Ni 4,435 |
Cu 3,50 |
Zn 1,35 |
Ga 2,78 |
Ge 3,87 |
As 3,0 |
Se 2,13 |
Br 1,22 |
Kr 0,116 |
|
Rb 0,858 |
Sr − |
Y 4,387 |
Zr 6,316 |
Nb 7,47 |
Mo 6,81 |
Tc − |
Ru 6,615 |
Rh 5,752 |
Pd 3,936 |
Ag 2,96 |
Cd 1,16 |
In 2,60 |
Sn 3,12 |
Sb 2,70 |
Te 2,6 |
− |
− |
|
Cs 0,827 |
Ba 1,86 |
La 4,491 |
Hf 6,35 |
Ta 8,089 |
W 8,66 |
Re 8,10 |
Os − |
Ir 6,93 |
Pt 5,852 |
Au 3,78 |
Hg 0,694 |
Tl 1,87 |
Pb 2,04 |
Bi 2,15 |
− |
− |
− |
Приведенные выше рассуждения, основанные на классических представлениях, достаточно хорошо описывают энергии связи для молекулярных и ионных кристаллов. В случае металлических и ковалентных связей, в которых конфигурации валентных электронов значительно отличаются от их конфигурации в изолированных атомах, такой подход не дает результатов, которые достаточно хорошо соответствовали бы экспериментальным. Здесь требуется привлечение квантовомеханических представлений.
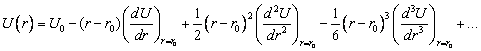
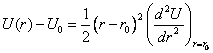
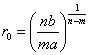 .
.