1.9.3. Экспериментальные методы определения структуры кристаллов
Падающие
под произвольным углом q на монокристалл рентгеновские лучи с длиной волны l в общем случае отражаться не будут, поскольку
неизвестными в системе (1.12) являются углы j, y и c, а квадраты косинусов этих углов связаны между собой
четвертым уравнением ![]() . Чтобы выполнялись условия Лауэ или закон Вульфа−Брэггов,
надо подобрать или длины волн, или углы падения. На основании этого подбора
были разработаны три основных метода получения дифракционной картины [46, 72,
78].
. Чтобы выполнялись условия Лауэ или закон Вульфа−Брэггов,
надо подобрать или длины волн, или углы падения. На основании этого подбора
были разработаны три основных метода получения дифракционной картины [46, 72,
78].
Метод
Лауэ
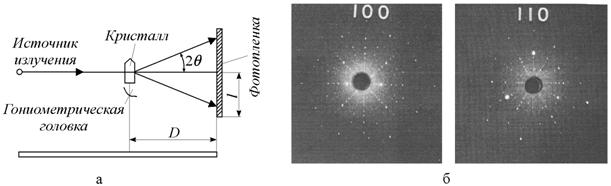
Немонохроматический пучок рентгеновских лучей (электронов или нейтронов) направляется на неподвижно закрепленный монокристалл (рис. 1.35, а).
|
|
|
Рис. 1.35. Дифракционный метод Лауэ: а - схема метода Лауэ; б − лауэграмма монокристалла пирита (FeS2) в двух ориентациях (100) и (110) [88] |
Кристалл «выбирает» те длины волн из всего их интервала, для которых удовлетворяется условие Вульфа−Брэггов. Плоская фотографическая пленка располагается так, что на нее попадают либо проходящие, либо отраженные дифрагированные пучки. Дифракционная картина состоит из серии симметрично расположенных пятен (рис. 1.35, б). Каждое пятно на лауэграмме соответствует плоскости решетки, ориентация которой полностью определяется направлением дифракционного луча.
Поскольку заранее неизвестны длины волн, составляющих различные отраженные пучки, то по лауэграмме нельзя определить размеры элементарной ячейки. Кристаллы с подобными ячейками и структурами, но с различными периодами элементарных ячеек будут давать одинаковые лауэграммы. Кроме того, одна и та же атомная плоскость может давать несколько отражений различных порядков, в результате чего некоторые пятна на лауэграмме могут оказаться результатом наложения нескольких отражений. Метод Лауэ используется кристаллографами в основном для определения элементов симметрии кристаллов, хорошо выявляющейся на снимках, а также для определения ориентировки кристаллов.
Метод
вращения монокристалла
Монокристалл
вращается вокруг какой-либо фиксированной оси, направление которой заранее
найдено методом Лауэ, в монохроматическом пучке рентгеновских лучей или
нейтронов. При повороте кристалла различные атомные плоскости занимают такие
положения, при которых отраженные от них лучи интерферируют. Вокруг
вращающегося кристалла помещают фотопленку в кассете, представляющей собой
цилиндр, ось которого совпадает с осью вращения кристалла.
Все
пучки, отраженные от плоскостей, параллельных вертикальной оси вращения, будут
лежать в горизонтальной плоскости. Плоскости с другими ориентациями будут
давать отражения, расположенные выше и ниже горизонтальной плоскости. Такое
расположение рефлексов отражения называют слоевыми линиями. Слоевую линию,
лежащую в плоскости первичного пучка, называют нулевой. Получающуюся
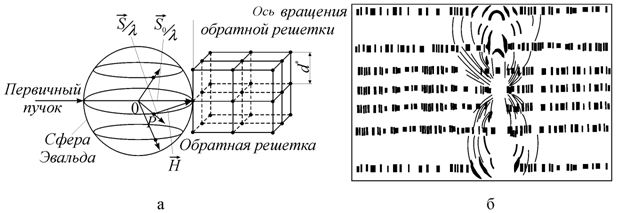
дифракционную картину легко объяснить с помощью сферы Эвальда (рис. 1.36).
Обратная решетка вращается, а сфера Эвальда неподвижна. В момент, когда
какой-либо узел обратной решетки выходит на поверхность сферы в направлении ![]() , из центра сферы к этой точке происходит отражение.
, из центра сферы к этой точке происходит отражение.
|
|
|
Рис. 1.36. Метод вращения монокристалла: а − схема возникновения интерференции в пространстве обратной
решетки; |
В
отличие от метода Лауэ, метод вращения монокристалла позволяет выяснить
структуру кристалла, т. е. установить форму и периоды элементарной ячейки, а в
некоторых случаях, найти координаты всех базисных атомов [75].
Используются
и разновидности метода вращения. Один из них − метод качания
монокристалла − предполагает поворот кристалла в ограниченном интервале
углов. В прецессионных камерах вместе с качанием кристалла происходит
перемещение пленки.
Метод порошка (Дебая)
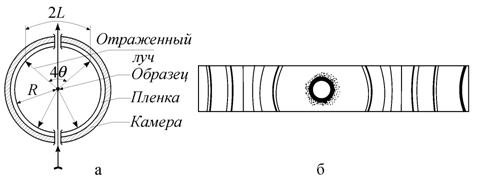
Пучок монохроматических лучей падает на поликристаллический образец. Падающие лучи отражаются от тех кристаллитов, которые по отношению к направлению падающего пучка оказываются ориентированы так, что выполняется условие Вульфа-Брэггов (1.10). Используется два способа регистрации дифракционной картины: на фотопленку (фотометод) (рис. 1.37, а) [74] и с помощью счетчика (дифрактометрический метод).
|
|
|
Рис. 1.37.
Дифракционный метод Дебая: а −
схема съемки поликристалла в цилиндрической камере (R − радиус камеры); б − рентгенограмма на фотопленке, полученная при съемке в цилиндрической камере |
Дифракционная картина на пленке выглядит в этом случае как серия концентрических окружностей (рис. 1.37, б).
Дифрактометр регистрирует картину в виде
чередования кривой фона и максимумов интерференции. Последние возникают на
определенных углах положения счетчика 2q. С помощью уравнения (1.10) по
измеренному значению угла рассеяния q можно рассчитать межплоскостные
расстояния ![]() для любого
дифракционного максимума. Далее делается предположение о типе кристаллической
структуры данного материала и определяются значения индексов полученных
отражений. Затем, если этот этап расчета выполнен, можно определить размеры
элементарной ячейки. Если известны химический состав и плотность материала,
рассчитывают количество атомов в элементарной ячейке. Наконец, по интегральной
интенсивности дифракционных линий можно установить детальное расположение
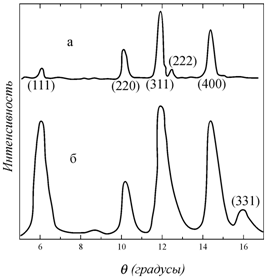
атомов в элементарной ячейке. На рис. 1.38 в качестве примера приведены
зависимости интенсивности от угла рассеяния для поликристалла магнетита (Fe3O4), полученные
методом дифракции рентгеновских лучей (верхняя кривая) и нейтронов (нижняя
кривая).
для любого
дифракционного максимума. Далее делается предположение о типе кристаллической
структуры данного материала и определяются значения индексов полученных
отражений. Затем, если этот этап расчета выполнен, можно определить размеры
элементарной ячейки. Если известны химический состав и плотность материала,
рассчитывают количество атомов в элементарной ячейке. Наконец, по интегральной
интенсивности дифракционных линий можно установить детальное расположение
атомов в элементарной ячейке. На рис. 1.38 в качестве примера приведены
зависимости интенсивности от угла рассеяния для поликристалла магнетита (Fe3O4), полученные
методом дифракции рентгеновских лучей (верхняя кривая) и нейтронов (нижняя
кривая).
|
|
|
Рис. 1.38. Дифракционная картина рассеяния а − рентгеновских
лучей и б − нейтроннов поликристаллом магнетита (Fe3O4) (в скобках указаны индексы дифракционных максимумов) [88] |
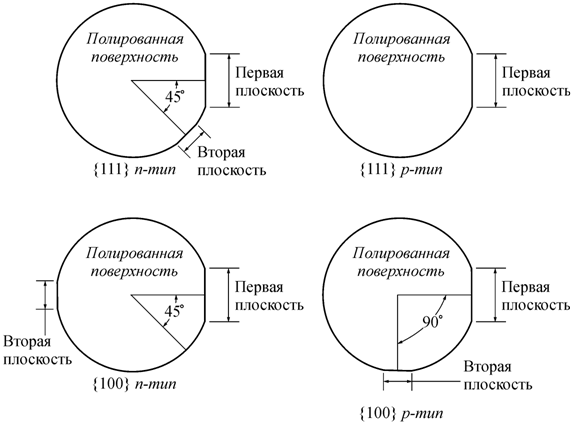
Кроме перечисленных выше методов, где основой получения данных о структуре кристаллов выступает явление дифракции коротковолновых излучений на кристаллической решетке, в технике часто используется специальная маркировка кристаллов, позволяющая установить, например, плоскость, по которой вырезан данный кристалл. На рис. 1.39 показано, как при помощи соответствующих геометрических элементов монокристальных пластин кремния, выращиваемых для создания больших интегральных схем, можно установить плоскость, вдоль которой вырезан монокристалл и тип полупроводника (n или p – тип).
|
|
|
Рис. 1.39. Идентификация
плоскостей в кремниевых монокристальных пластинах [97] |