1.9.2. Дифракция рентгеновских лучей в кристаллах

Падающая на атом вещества электромагнитная волна рентгеновского излучения вызывает индуцированные колебания электронов. При этом излучается электромагнитная волна с той же частотой, с какой происходят колебания. Излучаемая электроном волна имеет сферический фронт, в центре которого находится осциллирующий диполь. Таким образом, волна рассеивается по всем направлениям. Этот процесс поглощения энергии падающего излучения и отдачи этой энергии при испускании сферической волны той же длины называется когерентным рассеянием падающего излучения. Зная распределение электронов в атоме, можно теоретически рассчитать рассеивающую способность атома. В реальном теле атомов огромное количество, и в падающий пучок рентгеновских лучей всегда попадает большое их число. Каждый из атомов становится источником рассеянных волн, которые в результате интерференции могут усиливать или ослаблять друг друга. Это означает, что энергия излучения рассеивается в разных направлениях с различной интенсивностью. Вид картины рассеяния будет зависеть от сорта атомов, расстояний между ними, частоты падающего излучения и ряда других факторов [46].

Русский ученый Вульф и англичане, отец и сын Брегги, дали простое толкование интерференции рентгеновских лучей в кристаллах, объяснив ее отражением от атомных сеток.

Пусть на кристалл под углом скольжения q, падает параллельный пучок монохроматических рентгеновских лучей с длиной волны l (рис. 1.32). Лучи отражаются от параллельного поверхности семейства плоскостей с межплоскостным расстоянием d под таким же углом q. Параллельные отраженные лучи I и II интерферируют, т. е. усиливают и ослабляют друг друга. Если их разность хода  равна целому числу n длин волн l, то наблюдается интерференционный максимум. Условие возникновения такого максимума можно записать в виде

.

(1.10)

Соотношение (1.10) носит название формулы Вульфа−Брэггов. Закон Вульфа−Брэггов является следствием периодичности пространственной решетки и не связан с расположением атомов в ячейке или в узлах решетки.

 

Рис. 1.32. К выводу формулы Вульфа−Брэггов

 

Условия Лауэ

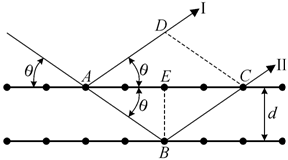
Лауэ определил условия, при которых возникают интерференционные максимумы при рассеянии излучения на узлах кристаллической решетки. Выделим в кристалле узловой ряд в направлении оси x с расстоянием между узлами а (рис. 1.33). Если на такой ряд направить под произвольным углом  пучок параллельных монохроматических лучей с длиной волны l, то интерференционный максимум будет наблюдаться только в направлениях, для которых все отражения от узлов усиливают друг друга.

 

Рис. 1.33. К выводу уравнения Лауэ

 

Обозначим разность хода между падающим и рассеянным каким-либо узлом ряда лучом . Ее также можно выразить через период ряда и косинусы углов, образуемых этими лучами с линией, связывающей узлы:

,

(1.11)

где целое число h – индекс интерференции.

Если рассмотреть условия Лауэ для трех некомпланарных направлений , то они будут иметь вид

, , ,

(1.12)

где ,  − углы падения  рентгеновских лучей на узловые ряды, располагающиеся вдоль направлений  соответственно, а k, l − соответствующие индексы интерференции.

Используя понятие обратной решетки и обозначив вектор обратной решетки , уравнения Лауэ (1.12) можно заменить одним интерференционным уравнением. Для этого докажем тождество

,

(1.13)

где  − осевые векторы прямой решетки,  − соответствующие векторы обратной решетки. Вектор обратной решетки , как было показано выше, можно представить в виде

.

(1.14)

Умножим правую и левую части этого выражения сначала на , потом на  и на  соответственно. ; ; , т. к.

.

Это означает, что тождество (1.13) действительно верно.

Если обозначить как  единичные векторы, характеризующие направления падающего и рассеянного лучей, то ,  и 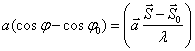. Тогда условия (1.12) можно записать в виде

; ; .

(1.15)

Умножим правую и левую части этих уравнений соответственно на  и сложим их.

.

(1.16)

Учитывая тождество (1.13), получим интерференционное уравнение

.

(1.17)

Это уравнение полностью определяет положение максимумов интерференции и заключает в себе как условие Лауэ, так и условие Вульфа−Брэггов: интерференционный максимум наблюдается тогда, когда дифракционный вектор , по длине и направлению совпадает с вектором обратной решетки .

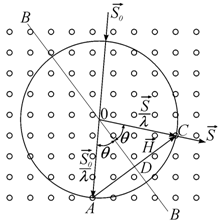
Проиллюстрируем геометрически интерференционное уравнение в двумерном случае (рис. 1.34). Такое построение называется построением Эвальда.

 

Рис. 1.34. Окружность отражений Эвальда во взаимодействии с плоской обратной решеткой (ВВ – след плоскости (hkl), вектор  ей перпендикулярен, q – брэгговский угол)

 

На двумерную решетку с известными периодами а и b и углом между ними g в направлении  падает плоская монохроматическая волна с длиной l. Определим периоды обратной решетки  и построим ее в масштабе . Выберем произвольный узел А и из него в направлении, обратном , отложим отрезок  до точки 0. Из этой точки опишем окружность радиусом  (точка 0 не обязательно попадает в какой-либо узел). Все узлы, попавшие на окружность, находятся в отражающем положении. На рис. 1.34 таким узлом является узел С. Для каждого подобного узла три вектора ; ;  удовлетворяют уравнению (1.17).

Покажем теперь, что интерференционное уравнение Лауэ и закон Вульфа−Брэггов эквивалентны друг другу. Векторы  и  (рис. 1.34) определяют соответственно направления падающего и интерференционного лучей .

Рассмотрим треугольник OAD, в котором сторона . Поскольку из уравнения (1.9) длина вектора обратной решетки обратна значению межплоскостного расстояния , то . Определим из треугольника OAD угол q.

.

Тогда .

Таким образом, условие возникновения интерференционного максимума Вульфа−Брэггов выполняется для узла, попавшего на окружность отражения.

В трех измерения построения представляют собой сферу Эвальда. Такое построение позволяет определить направление интерференционных лучей и индексы узлов обратной решетки , которые соответствуют отражающему семейству плоскостей (HKL) прямой решетки.
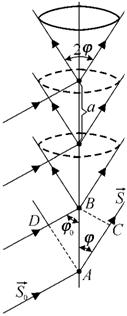
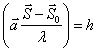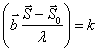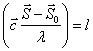