1.4. Обратная решетка
В физике твердого тела при анализе многих явлений (дифракция, движение электронов в потенциальном поле, рассеяние фотонов), связанных с периодическим расположением частиц, важную и полезную роль играет обратная решетка.
Обратная решетка представляет собой удобную абстракцию, позволяющую математически просто описать условия протекания того или иного явления в твердом кристаллическом теле.
Между векторами элементарных трансляций и параметрами обратной решетки существует вполне определенная связь.
Пусть в кристаллической решетке
элементарная ячейка определяется тремя элементарными трансляциями 
, 
, 
(рис. 1.14) [75].
Простейшими плоскими сетками являются сами координатные плоскости. Семейство
плоскостей, параллельных векторам 
и 
(или, другими словами,
плоскости семейства (100)), можно изобразить точкой на конце некоторого вектора
, перпендикулярного к этим плоскостям. За длину этого вектора
примем величину, обратную соответствующему межплоскостному расстоянию 
. Здесь 
− проекция
вектора 
на нормаль к плоскости
(100). Длину вектора можно определить из
условия:
|
|
(1.1) |
.Кроме того, вектор откладывается вдоль
нормали к плоскости так, чтобы для наблюдателя, смотрящего вдоль направления , вращение от к совершалось по часовой
стрелке.
В векторном виде эти условия записываются тремя скалярными произведениями:
|
|
(1.2) |
.Два других вектора 
и 
определяют, исходя из
сеток на других координатных плоскостях:
|
|
(1.3) |
|
|
|
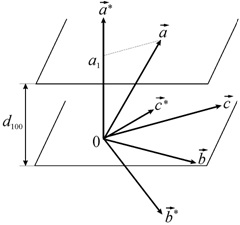
Рис. 1.14. К выводу связи между параметрами прямой и обратной решеток |
Проведем три вектора , и из какой-либо
произвольной точки, которую назовем началом координат обратного пространства.
Точечная решетка, построенная на этих векторах, является обратной решеткой для исходной (прямой) решетки кристалла.
Пусть объем элементарной ячейки
прямой решетки 
, тогда
|
|
(1.4) |
,откуда в соответствии с соотношениями (1.1), (1.2) и (1.3)
|
|
(1.5) |
.Углы между каждой парой векторов , , обозначим 
. Они равны по величине двугранным углам триэдра,
построенного на векторах , , , и могут быть вычислены из углов 
между векторами прямой
решетки по формулам:
|
|
(1.6) |
|
|
|
|
|
,
,
.Если в кристаллической решетке все
углы прямые, то вектора элементарных трансляций , , обратной решетки
параллельны векторам , , прямой решетки и
обратны им по величине. К этому результату можно прийти из формулы (1.5).
Действительно, в этом случае объем элементарной ячейки 
, а векторное произведение 
. Поэтому 
.
Объем элементарной ячейки обратной решетки равен
|
|
(1.7) |
,откуда
|
|
(1.8) |
.Таким образом, объем элементарной
ячейки обратной решетки 
есть величина обратная
объему элементарной ячейки ристалла. Это соотношение является общим и применимо
ко всем кристаллическим решеткам, в том числе и к непрямоугольным.
Любой вектор обратной решетки 
перпендикулярен плоскости
прямой кристаллической решетки 
, а длина его является величиной обратной межплоскостному
расстоянию:
|
|
(1.9) |
.Итак, прямая и обратная ячейки взаимно сопряжены. Если для описания кристаллической решетки вместо принятой вначале выбрать другую элементарную ячейку, то для обратной решетки получится также другая группа из трех векторов, но решетка, построенная таким образом, будет идентична первой. Это следует из прямой связи между любым вектором одной решетки с одним только семейством плоскостей другой вне зависимости от координатных осей. Соответствие между двумя решетками, их взаимосвязь не зависят от выбора элементарной ячейки.
Решетка, обратная обратной решетке, является исходной (прямой) решеткой.
Каждый узел [[HKL]]* обратной решетки соответствует семейству параллельных плоскостей (HKL) прямой решетки.
Обратная решетка сама является (по отношению
к конкретной решетке Бравэ) решеткой Бравэ. Так, для примитивной кубической
ячейки Бравэ со стороной а обратной
является примитивная кубическая ячейка Бравэ со стороной 
. Обратная к гранецентрированной есть объемноцентрированная
решетка, а прямой объемноцентрированной соответствует обратная
гранецентрированная.
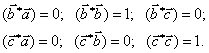
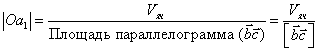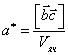