1.3.2. Пространственные группы симметрии

Построение решетки кристалла путем трансляции элементарной ячейки - это наиболее простой подход к решению данной задачи. Оказалось, что весь кристалл, в узлах кристаллической решетки которого находятся центры атомов одного и того же сорта, можно построить, исходя не из всей ячейки, а из единственного атома, повторяя его при помощи операций симметрии пространственной группы.

В пространственной группе к элементам симметрии точечной группы добавляются операции трансляций. Всего пространственных групп 230. Если система точек представляет собой решетку Бравэ, то каждую поворотную ось симметрии можно заменить винтовой, а каждую плоскость симметрии – плоскостью скользящего отражения.

К пространственным элементам симметрии относятся винтовые оси симметрии. Винтовые оси симметрии характеризуют, например, расположение чешуек еловой шишки. У шпильки бесконечной длины с резьбой имеется винтовая ось симметрии бесконечного порядка, а у винта с шестигранной головкой − винтовая ось шестого порядка. По аналогии с простыми инверсионными и зеркально-поворотными осями оси симметрии кристаллической структуры могут быть только двойными, тройными, четверными и шестерными. Различают правые и левые винтовые оси. Для правой оси перемещение вдоль нее сопряжено с поворотом по часовой стрелке, а для левой − против часовой стрелки.

Винтовые оси обозначают цифрой, равной порядку оси с добавлением индекса внизу (табл. 1.4) [83]. Частное от деления цифры, стоящей в индексе, на порядок оси дает величину переноса вдоль оси, выраженную через элементарную трансляцию вдоль этой оси. Дробь в табл. 1.4 показывает, на какую долю трансляционного вектора , совпадающего по направлению с винтовой осью, смещается точка после поворота на соответствующий угол вокруг оси.

Таблица 1.4

Винтовые оси симметрии и их обозначения

 

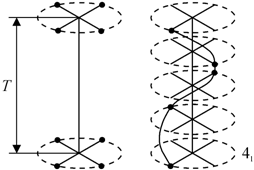
Операция трансляции четверной винтовой осью  показана на рис. 1.13. Видно, что для нее возможны трансляции , результаты которых показаны на правом рисунке точками. При этом поворот вокруг оси трансляции совершается по часовой стрелке. В первом случае осуществляется поворот вокруг оси на  и смещение на ¼ трансляционного вектора, во втором − поворот на  со смещением, составляющим половину трансляции, и в третьем − поворот на  с трансляцией на ¾  длины вектора .

 

Рис. 1.13. Операции трансляции винтовой осью

 

Вторая операция симметрии - плоскость скользящего отражения. Она комбинирует операцию отражения в совокупности с трансляцией вдоль соответствующего направления, или, иначе, со скольжением. При этом перенос производится на величину, равную половине периода трансляции , либо .

Плоскости скользящего отражения с трансляцией  называют клино-плоскостями, а с трансляцией  - плоскостями алмазного скольжения.

Таким образом, пространственные группы определяют природу элементов симметрии, создающих калейдоскоп, размножающий характерный для структуры мотив. Это позволяет построить не только элементарную ячейку, но и весь периодический кристалл. Система точек, получающаяся из одной точки путем повторения ее всеми элементами симметрии пространственной группы, называется правильной системой точек.

Если размножаемая пространственной группой точка не лежит на элементе симметрии, то говорят, что она находится в общем положении, если лежит, – то в частном положении.