1.3.1. Точечные операции симметрии

Воображаемые точки, линии и плоскости, с помощью которых осуществляются упомянутые операции вращения и отражения, называются элементами симметрии. В кристаллографии для обозначения операций симметрии и соответствующих им элементов симметрии служат специальные символы. Наиболее распространенными из них являются международные символы, принятые Интернациональным союзом кристаллографов, и символика, основанная на формулах симметрии [27]. Перечислим элементы и связанные с ними операции симметрии.

Центр симметрии (центр инверсии) − это некая воображаемая точка внутри кристаллической  решетки, характеризующаяся тем, что любая прямая, проведенная через нее, встречает идентичные друг другу узлы решетки на равных расстояниях от центра. Симметричное преобразование в центре симметрии − это зеркальное отражение кристаллической решетки в точке. Обозначается центр симметрии буквой C.

Поворотные оси симметрии представляют собой прямые линии, при повороте вокруг которых на некоторый определенный угол кристаллическая решетка совмещается сама с собой.  По формуле симметрии поворотные оси обозначают буквами , где n - порядок оси, который может принимать значения только 1; 2; 3; 4; 6. Порядок оси симметрии n показывает, сколько раз решетка совместится сама с собой при полном повороте вокруг этой оси. Таким образом, поворотные оси определяют вращение вокруг них на углы  (первый порядок), 2p/2 (второй порядок), 2p/3 (третий порядок), 2p/4 (четвертый порядок), 2p/6 (шестой порядок), которое приводит к совмещению решетки с самой собой. Геометрические обозначения поворотных осей различных порядков приведены в табл. 1.3. Следует особо отметить, что в кристаллах невозможны оси симметрии 5-го порядка и порядка, большего чем 6. Это ограничение связано с тем, что в кристаллическом состоянии вещество представляет собой систему материальных частиц, симметрично повторяющихся в пространстве. Такие симметричные ряды, непрерывно заполняющие пространство, несовместимы с осями 5-го, 7-го и других порядков. Доказательство этого утверждения можно обнаружить в любом учебнике по кристаллографии.

Плоскости зеркального отражения  делят фигуру на две части, расположенные друг относительно друга как предмет и его зеркальное отражение. В интернациональной системе плоскость зеркального отражения принято обозначать  символом m или P по формуле симметрии.

Совокупностью P, C, , , ,  (табл. 1.3) исчерпываются все возможные точечные операции симметрии первого рода.

Точечные операции симметрии второго рода представляют собой совместное действие двух операций симметрии: вращение и инверсия в центре симметрии или вращение и отражение в плоскости симметрии.

Инверсионная ось симметрии представляет собой сочетание поворота вокруг оси вращения на угол  с одновременным отражением в центре симметрии.

Имеются инверсионные оси первого, второго, третьего, четвертого и шестого порядка (обозначения в международной символике − ). Инверсионная ось первого порядка  эквивалентна центру симметрии C, а второго  – плоскости симметрии P. Инверсионная ось  всегда одновременно является поворотной осью  (но не наоборот). Инверсионная ось может рассматриваться как совокупность отдельно действующих оси  и центра инверсии C.

Кроме инверсионных осей, в точечных операциях симметрии второго рода иногда пользуются так называемыми зеркально-поворотными осями симметрии, которые представляют собой сочетание оси симметрии и отражения в плоскости симметрии, перпендикулярной этой оси. Однако в международной символике эти операции симметрии не указываются, поскольку все зеркально-поворотные оси, возможные в кристаллах, можно заменить инверсионными осями симметрии.

Полный список точечных операций симметрии и их обозначений приведен в табл. 1.3 [83].

 

Таблица 1.3

Элементы симметрии и их обозначения

 

Совокупность операций симметрии, осуществленных относительно какой-либо точки решетки, в результате чего решетка совмещается сама с собой, называется точечной группой, или классом симметрии кристаллической решетки.

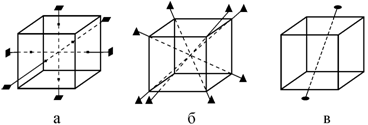
В качестве примера рассмотрим оси симметрии кубической решетки (рис. 1.12). У куба имеется:

− три оси четвертого порядка (), проходящие через центры противоположных граней (рис. 1.12, а);

− четыре оси третьего порядка (), которые являются пространственными диагоналями куба (рис. 1.12, б);

− шесть осей второго порядка (), проходящих через середины пар противоположных ребер (рис. 1.12, в).

 

Рис. 1.12. Оси симметрии кубической решетки: а – оси четвертого порядка, б – третьего, в − второго (показана одна из шести)

 

Все оси симметрии куба пересекаются в одной точке − в центре куба.