1.2.1. Элементарная ячейка. Базис решетки

Одним из основных представлений, связанных со структурой кристаллов, является понятие об элементарной ячейке. В общем случае элементарную ячейку можно представить, как минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку.

Закономерности строения элементарной ячейки, в частности степень их симметричности определяет многие свойства кристалла, в первую очередь электрические, магнитные и механические. Элементарная ячейка может содержать как один, так и несколько атомов. Так у многих металлов, например железа, хрома, меди, серебра, она состоит из одного атома. В тех случаях когда, кристалл состоит из нескольких химических элементов, например, натрия и хлора, элементарная ячейка будет содержать два атома: натрий и хлор. Широко распространены кристаллы с элементарной ячейкой, состоящей из нескольких сцепленных друг с другом молекулярных групп, например кристаллы льда или же многих магнитных материалов. Существуют кристаллы, например, белковые, элементарная ячейка которых состоит из молекул, содержащих несколько тысяч атомов.

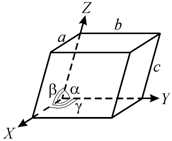
Один из способов построения пространственной решетки состоит в трансляции (размножении) элементарной ячейки, имеющей вид элементарного параллелепипеда, построенного на трех некомпланарных векторах , называемых векторами основных трансляций (рис. 1.5). За начало этих векторов можно принять любую точку. Модули векторов , ,  называются периодами элементарной ячейки, а углы между ними a, b, g  - углами элементарной ячейки. Если весь параллелепипед построен на основных трансляциях a, b, c, то элементарная ячейка называется примитивной (обозначается буквой P). Примитивная элементарная ячейка не имеет дополнительных узлов ни внутри себя, ни на поверхности.

Каждый узел, находящийся в вершине элементарной ячейки, принадлежит еще восьми соседним элементарным ячейкам. Поскольку всего узлов (или вершин параллелепипеда) восемь, то () и на примитивную элементарную ячейку приходится всего один узел.

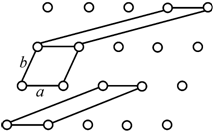
Казалось бы, что выбор элементарной ячейки произволен. На рис. 1.6 все три плоские ячейки примитивны. Хотя трансляции в двух из них и не являются кратчайшими, но любая из них воспроизводит при переносе параллельно самой себе в двух направлениях всю «структуру кристалла». Однако Бравэ были сформулированы 3 правила выбора элементарных ячеек, выполняемые в указанной ниже последовательности.

1.      Симметрия элементарной ячейки должна соответствовать симметрии кристалла.

2.      Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.

3.      При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.

При выполнении этих правил элементарная ячейка, в отличие от примитивной, кроме узлов в вершинах, может иметь дополнительные узлы.

 

Рис. 1.5. Элементарная ячейка	Рис. 1.6. Различные способы выбора элементарных ячеек

 

Совокупность координат всех узлов, приходящихся на элементарную ячейку, часто называют ее базисом. Сложную ячейку обычно выбирают так, чтобы узлы находились либо в центрах граней, либо в центре объема. Поэтому принята система наиболее распространенных видов сложных ячеек.

Приведем примеры сложных элементарных ячеек в узлах которых находятся атомы одного сорта.

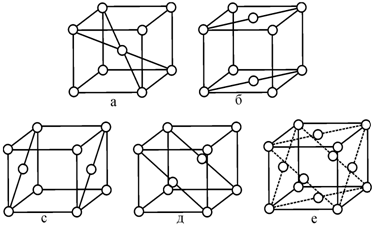
Объемноцентрированная ячейка (обозначается буквой I) (рис. 1.7, a). Кроме узла, находящегося в начале координат, она имеет дополнительный узел, расположенный на пересечении телесных диагоналей. Таким образом, на данную элементарную ячейку приходится всего два узла и ее базис [[000]], [[½ ½ ½]].

Базоцентрированная ячейка (обозначается буквой С) (рис. 1.7, б), так же как и объемноцентрированная, характеризуется базисом из двух узлов, индексы которых [[000]], [[½ ½ 0]]. На рисунке видно, что в этой ячейке дополнительные узлы находятся в центрах граней, перпендикулярных оси c. Ясно, что данные узлы принадлежат этой ячейке только наполовину, но т. к. таких граней в ячейке две, то ей принадлежит один узел, находящийся на грани.

Бокоцентрированная ячейка. Возможны два варианта: А-ячейка, в которой центрирована грань, перпендикулярная оси а, и В-ячейка, где дополнительные узлы находятся в центре граней, перпендикулярных оси b, базисы которых соответственно: А − [[000]], [[0 ½ ½]] (рис. 1.7, г), B − [[000]], [[½ 0 ½]] (рис. 1.7, в).

Гранецентрированная ячейка (рис. 1.7, д) (обозначается буквой F). Дополнительные узлы находятся в центрах граней. Общее число узлов, приходящихся на гранецентрированную ячейку, четыре. Ее базис [[000]], [[0 ½ ½]], [[½ 0 ½]], [[½ ½ 0]].

 

Рис. 1.7. Примеры элементарных ячеек