Для рентгеновских лучей, электронов и нейтронов, длины волн которых соизмеримы с межатомными расстояниями, то есть лежат в диапазоне от 0.5 до 3.0 Å, кристаллы служат трехмерными дифракционными решетками.
Рассмотрим рассеяние одномерной цепочки атомов (рис. 10).
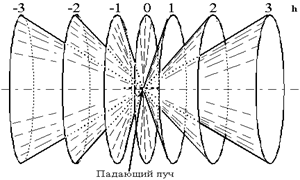
Рис. 10. Дифракционные конусы, возникающие при рассеянии цепочкой атомов.
Пусть на цепочку атомов с межатомным расстоянием (периодом трансляции) a падает под углом α0 плоская волна. Каждый атом становится источником сферической рассеянной волны. Расстояние между атомами на несколько порядков меньше, чем расстояние от источника падающего излучения до цепочки атомов и от рассеивающих атомов до регистрирующего устройства (пленка или счетчик). Поэтому фронты падающих и рассеяных волн можно рассматривать как плоские.
Разность хода лучей, рассеянных соседними атомами, определяется как а(cosα - cosα0), и в направлениях, в которых она равна целому (h) числу длин волн λ, рассеянные волны при интерференции максимально усилят друг друга. В силу сферичности рассеянных атомами волн максимумы возникнут по всем образующим дифракционного конуса с углом раствора 2α.
Из формулы
a(cosα - cosα0) = hλ (1)
следует, что каждому целому значению числа h, удовлетворяющему условию h ≤ λ/2а, будет соответствовать свой дифракционный конус.
Если рассеивает атомная плоскость, то ее можно рассматривать как совокупность двух пересекающихся атомных цепочек с периодами трансляций a и b , каждая из которых дает свою систему дифракционных конусов. Интенсивность будет максимальной в тех направлениях, где дифракционные конусы пересекаются попарно, т.е. выполняются условия:
a(cosα - cosα0) = hλ
b(cosβ - cosβ0) = kλ (2)
Трехмерная периодическая решетка кристалла полностью определяется тремя атомными цепочками, параллельными координатным осям. В этом случае можно записать три соотношения:
a(cosα - cosα0) = hλ
b(cosβ - cosβ0) = kλ
c(cosγ - cosγ0) = lλ (3)
где a, b, c – периоды решетки по трем некомпланарным направлениям, принятым за оси координат; h, k, l – целые числа, равные 0, ± 1, ± 2,.... Углы, составляемые дифрагированным и падающим лучами с осями координат, обозначены как α, β, γ и α0, β0, γ0 соответственно.
Соотношения (1), (2), (3) представляют собой условия Лауэ для одно-, двух- и трехмерной решеток соответственно.
Каждое из трех условий (3) определяет семейство конусов, аналогичное представленному на рис.10, для осей (x,y,z). Одновременное выполнение всех трех условий (3) при заданных индексах h, k, l означает, что для появления дифракционного максимума три конуса должны пересечься по одному направлению. Ясно, что в общем случае такое пересечение не имеет места (рис. 11), поскольку растворы конусов, определяемые периодами а, b, с независимы друг от друга и пересекаются лишь попарно. Встает вопрос о том, как в этом случае получить дифракционную картину?
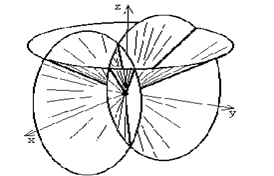
Рис. 11 . Дифракционные конусы при рассеянии на трехмерной решетке.
В уравнениях Лауэ (3) величины а, b, с характеризуют данный кристалл и не меняются в процессе его исследований. Углы α0, β0, γ0 определяют направление падающих лучей, и их можно точно задать, равно как и фиксировать величину длины волны λ падающего излучения. Поэтому на первый взгляд кажется, что в трех условиях Лауэ остается только три неизвестных величины, определяющих направление рассеянных лучей: α, β, γ, которые можно найти совместным решением уравнений. Однако это не так. На самом деле неизвестные α, β, γ не независимы. Для случая, когда пространственная решетка может быть описана прямоугольной системой координат, углы α, β, γ связаны между собой известным тригонометрическим соотношением:
cos2α + cos2β + cos2γ = 1 (4)
Для косоугольных координатных осей
cos2α + cos2β + cos2γ = d2(h2/a2 + k2/b2 + l2/c2) (5)
Таким образом, для нахождения трех неизвестных мы имеем уже 4 уравнения, которые в общем случае несовместны и общего решения не имеют. Это означает, что при произвольной взаимной ориентации падающих лучей и кристалла дифракцию можно и не наблюдать: три дифракционных конуса в общем случае не пересекаются по одной прямой. Чтобы одновременно могли пересечься по одной линии три дифракционных конуса, т.е. для получения дифракционного максимума, необходимо, не считая искомых углов α, β, γ, непрерывно изменять еще какую-либо из величин в условиях (3). Отсюда вытекают три основных метода получения дифракционной картины, используемых в структурном анализе:
- метод Лауэ;
- метод вращения монокристалла;
- метод поликристалла или метод Дебая.
При освещении монокристалла монохроматическим излучением для получения дифракционной картины необходимо непрерывно изменять углы характеризуют данный кристалл и не меняются в процессе его исследований. Углы α0, β0, γ0, что достигается вращением или колебанием монокристалла.
Наконец, последний метод наблюдения дифракции, метод Дебая, использует в отличие от 2-х первых не монокристаллический, а поликристаллический, т.е. состоящий из мелких ( ~10-3 см) монокристаллов (или кристаллитов) образец. Если в таком образце кристаллики ориентированы беспорядочно, то при освещении его параллельным пучком монохроматических рентгеновских лучей множество кристалликов окажется в положениях, удовлетворяющих условиям Лауэ (3), и возникнет дифракционная картина.
Дифракцию в поликристаллах проще всего объяснить, исходя из представлений, развитых Вульфом и Брэггами вскоре после открытия рентгеновских лучей. Они рассмотрели кристалл как совокупность (семейство) параллельных, расположенных на одинаковом расстоянии друг от друга, заполненных атомами плоскостей (так называемых плоских сеток). Таких семейств плоскостей в кристалле можно построить множество. Каждое семейство будет иметь свое межплоскостное расстояние d – кратчайшее расстояние между сетками, измеренное по направлению нормали, и свой символ (HKL), называемый индексами Миллера. Символ (HKL) (индексы Миллера) означает, что семейство параллельных плоскостей делит отрезок а на H частей, отрезок b на K частей, а отрезок с на L частей.
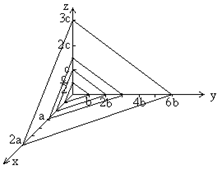
Рис.12. Семейство четырех параллельных плоскостей с символом (312).
Излучение, входя в кристалл на некоторую глубину, отражается от системы параллельных плоских сеток по законам геометрической оптики. При достаточной величине кристалла (не менее 10-5 см) в отражении примет участие очень большое число плоских сеток. Отраженные лучи, идущие по одному направлению, интерферируют между собой. Вследствие интерференции отраженный пучок будет обладать заметной интенсивностью только в том случае, если разность хода лучей, рассеянных двумя соседними плоскостями семейства, будет равна целому числу длин волн. Обозначим расстояние между плоскими сетками через d, а угол, составленный падающим лучом с плоской сеткой (угол скольжения), через θ. Разность хода Δ между лучами, рассеянными двумя ближайшими сетками, равна (см. рис. 13 ) Δ = ab + bc = 2dsinθ. Дифракционный максимум будет наблюдаться тогда, когда Δ равно целому числу длин волн, т. е. когда выполняется условие:
2dsinθ = nλ (6)
где n = 1, 2, 3... - порядок отражения.
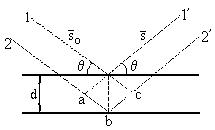
Рис. 13.
Формула (6) впервые была выведена крупнейшим русским кристаллографом Ю. В. Вульфом и англичанами отцом и сыном Брэггами. Формула Вульфа - Брэггов (6) лежит в основе дифракционных методов определения и анализа структуры кристаллов. С ее помощью можно рассчитать значения d/n = λ/2sinθ, так как в случае характеристического излучения длина волны λ известна заранее, а угол θ может быть определен экспериментально по дифракционной картине. В структурном анализе в формуле (6) n обычно принимают равным единице, так как отражение n-го порядка от семейства плоскостей с межплоскостным расстоянием d эквивалентно отражению первого порядка от семейства плоскостей с межплоскостным расстоянием d/n. Обозначают d/n = dhkl, где (hkl) - индексы интерференционного максимума, равные индексам Миллера (HKL) с точностью до целого числа n - порядка отражения.
Рассмотрим поликристалл, на который в направлении о-о падает пучок параллельных монохроматических лучей. В силу малости размеров составляющих поликристалл кристаллитов в облучаемом объеме их будет находиться множество: ~1011. Пусть в кристаллите (I) плоскости с межплоскостным расстоянием d1 находятся в отражающем положении. Как видно на рис. 5, дифрагированный этим кристалликом луч будет составлять угол 2θ1 с продолжением первичного пучка о-о. Если перпендикулярно направлению падающих лучей о-о поставить пленку, то на ней появится черная точка. Однако в образце найдутся и другие кристаллиты (например,I'), в которых плоскости с тем же межплоскостным расстоянием d1, составляя с осью о-о угол 2θ1, также будут находиться в отражающем положении, но ввиду беспорядочной ориентации окажутся иначе развернуты вокруг оси о-о. Дифрагированный кристалликом I' луч даст свою черную точку на пленке. В результате лучи, отраженные различным образом ориентированными вокруг оси о-о кристалликами, в которых плоскости с межплоскостным расстоянием d1 находятся в отражающем положении, заполнят в пространстве поверхность конуса с углом раствора 4θ1, и на пленке, перпендикулярной о-о, возникнет кольцо.
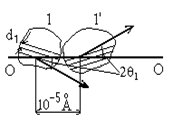
Рис. 14.
Кроме того, в поликристаллическом образце всегда есть кристаллики, которые также ока-жутся в отражающем положении, но в отражении будут участвовать плоские сетки другого семейства (другое значение d в уравнении (6)). Отраженные от таких кристалликов лучи образуют конус с другим углом раствора 4θ, и на пленке возникает второе кольцо.
В целом число дифракционных конусов и число колец на пленке зависит от числа различных по межплоскостным расстояниям систем атомных плоскостей, участвующих в отражении в различных кристалликах.
Если на пути дифракционных конусов перпендикулярно падающему пучку поставить фотопленку, то получим снимок в виде серии концентрических окружностей, расположенных вокруг центрального пятна, отвечающего месту пересечения пленки с падающим первичным пучком (рис. 15 ).
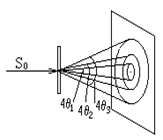
Рис. 15 . Дифракционная картина от поликристалла, полученная на плоскую пленку.
Как видно из рис. 15 , при таком расположении пленки улавливаются только дифракционные конусы с углами раствора в 4θ, меньшими 180°. Поэтому на практике пленку закладывают по поверхности цилиндра, вдоль оси которого устанавливается цилиндрический образец.
Следует подчеркнуть, что вид основных уравнений дифракции: условий Лауэ (4) и закона Вульфа - Брэггов (6), а также принципы методов получения дифракционной картины не зависят от природы падающего на кристалл излучения (рентгеновские лучи, электроны или нейтроны). Любую дифракционную картину вещества можно охарактеризовать числом и взаимным расположением линий, а также оценкой степени почернения (или площади) максимумов - интенсивности. Вид дифракционной картины определяется характером атомного расположения и индивидуален для каждого кристалла, поэтому значения межплоскостных расстояний dhkl, рассчитанные по формуле (6), и относительные (относительные интенсивности отражений: взятое в процентах отношение интенсивностей линий рентгенограммы к интенсивности самой сильной линии) интенсивности отражений являются "паспортом" кристалла и позволяют однозначно идентифицировать исследуемое вещество. Используемая для этой цели картотека JCPDS составлена по результатам анализа рентгенограмм кристаллов, поскольку рентгенографический метод получения дифракционной картины является наиболее простым в реализации.
Цилиндрические образцы исследуются в рентгеновских камерах Дебая (РКД).
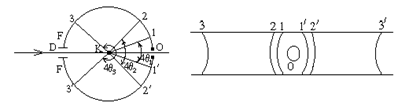
Рис. 16 . Ход лучей в камере Дебая (а); рентгенограмма (б).

Рис. 17 . Рентгенограмма алюминия.
На рис. 16 а показан ход лучей в камере Дебая. Здесь D – диафрагма, вырезающая в направлении к образцу K узкий пучок параллельных монохроматических лучей; 4θ1, 4θ2, 4θ3 и т.д. – углы раствора дифракционных конусов, пересекающихся с цилиндрической пленкой FOF по парным линиям 1-1', 2-2', 3-3' и т.д. (рис. 16 б); О – отверстие в пленке для выхода лучей, прошедших через образец без отклонения.
Расчет рентгенограмм сводится к определению углов θi и нахождению значений межплоскостных расстояний d/n = dhkl по формуле Вульфа - Брэггов (6). Углы θi определяют, исходя из того, что расстояние между парой симметричных линий 2Li равно дуге окружности, отвечающей углу 4θi радиан (рис.7 а):
2Li = 4θiR (R - радиус камеры) (7)
или в градусном измерении:
2Li = 4θi2πR/360 -> θi = 2Li57.3/2D (8)
Так как используемые камеры имеют диаметр D = 57.3 мм, то расстояние между двумя симметричными линиями будет равно удвоенному углу θ:
2θi = 2Li -> θi = Li (9)
Однако прежде чем переходить к вычислению межплоскостных расстояний d, необходимо учесть, что характеристическое излучение К серии, применяемое в данной работе, состоит из двух групп линий: Kα и Kβ. Kα -излучение представляет собой дублет α1 и α2, но ввиду того, что длины волн λ-Kα1 и λ-Kα2 разнятся очень мало, в камере Дебая расщепление этого дублета незаметно, и можно считать эти две линии за одну со средневзвешенным значением длины волны, равным:
λα = (2λKα1 + λKα2)/3 (10)
Kβ - излучение более коротковолновое и менее интенсивное, чем Kα. Следствием того, что используемое излучение представляет собой две спектральные линии, будет наличие на рентгенограмме совокупности двух систем линий: одна обусловлена α-, а другая - β-излучениями. Поэтому до расчета dhkl, необходимо отделить β-линии от α-линий. Если число β -линий не очень велико, то их можн исключить следующим образом.. Во-первых, β-линии по интенсивности в 7 раз слабее соответствующих α-линий, во-вторых, β-излучение более коротковолновое, поэтому для плоскостей с одним и тем же межплоскостным расстоянием dhkl β-линии будут иметь меньшие, чем α-линии, углы рассеяния 2θ. Первая линия рентгенограммы, как правило, является β-линией, следующая за ней - α-линией от того же самого семейства плоскостей (HKL). Кроме того, из (6) следует, что
sinθβ/sinθα = λβ/Λα (11)
Экспериментально установлено, что λβ/Λα = 0.9. Это соотношение должно выполняться лишь для линий с одинаковыми значениями dhkl. Из них ближайшая к центру будет β-линия. Отделив таким образом α-линии от β-линий, для каждой линии (как α , так и β) вычисляют значения межплоскостных расстояний dhkl по формуле Вульфа - Брэггов. Из двух значений dhkl (одно α-, а другое β-) берут среднее арифметическое. Найденные значения dhkl выписывают в порядке убывания и, сравнив с таблицей межплоскостных расстояний различных веществ или используя картотеку JPCDS, идентифицируют исследуемое вещество.
Сравнение экспериментальных значений dhkl с табличными данными производится с учетом ошибки эксперимента.
Дифференцирование уравнения (6) дает:
|Δd/d| = ctgθΔθ (12)
Таким образом, относительная погрешность в определении межплоскостных расстояний Δd/d пропорциональна абсолютной ошибке в определении угла Δθ, выраженной в радианах. Если величина Δθ постоянна для всех линий рентгенограммы, то Δd/d будет меньше для последних отражений, стремясь к нулю при θ, равном 90°.
Определив индексы (hkl) всех отражений, из dhkl можно рассчитать значения периодов элементарной ячейки ahkl по формуле:
ahkl = dhkl ![]() (13)
(13)
Поскольку Δd/d стремится к нулю при θ, приближающемся к 90°, то ясно, что Δahkl = Δdhkl также будет стремиться к нулю при θ, приближающемся к 90°. Следовательно, для получения истинных значений периода элементарной ячейки необходимо найти величину a = ahkl, соответствующую θ = 90°. Показано, что с учетом систематических ошибок, обусловленных неточностью юстировки образца и поглощением в тонком поверхностном слое, для нахождения периода a нужно построить зависимость ahkl от cos2θ. Экстраполяция этой зависимости к cos2θ = 0 даст истинное значение периода элементарной ячейки a. Указанный метод определения точного значения периода элементарной ячейки называется методом экстраполяции.
используются образцы из проволоки, изготовленной из металлов с кубической структурой. Известно, что все металлы кристаллизуются в трех типах решеток: гексагональной и двух кубических – объемно- и гранецентрированной (рис.18).
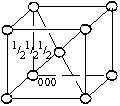
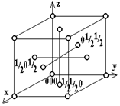
Рис. 18 . Объемно- и гранецентрированная кубические ячейки. Указаны координаты базисных атомов.
Если плотность исследуемого вещества известна, то, определив из эксперимента указанным выше способом значения периода a, можно рассчитать объем элементарной ячейки V:
V = a310-24 см3 (14)
Затем, найдя по таблице Менделеева атомный вес исследуемого элемента и умножив его на атомную единицу массы (а.е.м.=1.66 10-24г.), получим массу атома (m) исследуемого вещества в граммах. Величины V и m связаны с плотностью материала ρ (г/см3) и числом базисных атомов N соотношением:
ρ = Nm/V (15)
Целью работы является получение рентгенограмм металлов с объемно- и гранецентрированной кубическими решетками на двух излучениях с различными длинами волн. Необходимо: проанализировать зависимость дифракционной картины от типа кубической решетки и от длины волны падающего излучения; определить периоды кристаллической решетки для исследуемых металлов; рассчитать плотность материала ρ, зная число базисных атомов N и рассчитать число атомов в ячейке N, зная плотность ρ материала.
- Пользуясь указаниями, которые даны в описании к камере, установить и отцентрировать исследуемый образец.
- Перенести камеру на столик напротив окна рентгеновской трубки и при выключенном аппарате установить входной тубус камеры напротив окна трубки, выходной тубус при этом окажется несколько ниже. Схема установки камеры приводится на рис. 19 .
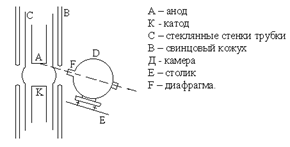
Рис. 19.Схема установки камеры Дебая около окна рентгеновской трубки. - Включить аппарат и произвести окончательную установку камеры, наблюдая за свечением флуоресцирующего экранчика в заглушке камеры: светящееся пятно от прошедшего рентгеновского пучка должно быть в центре экранчика, а тень от образца должна делить его пополам (см. рис. 20 ).

Рис. 20 . Схема расположения тени от образца на светящемся экране. - Закрыть шторкой окно, забрать камеру и в фотокомнате произвести зарядку камеры пленкой. Пленка вырезается по шаблону, для входа рентгеновских лучей дыроколом пробивается отверстие. Подготовлен-ную пленку осторожно, чтобы не сбить образец, вставить в камеру, плотно закрыть крышку камеры, и камеру перенести на столик к рентгеновской трубке.
- Открыть шторку и проверить по флуоресцирующему экранчику правильность установки образца и камеры. Убедившись в правильности установки камеры, экспонировать пленку в течение времени, указанного преподавателем или инженером.
- После окончания экспозиции закрыть шторкой окно, забрать камеру в фотокомнату. Проявить и отфиксировать пленку, тщательно промыть в проточной воде и высушить на воздухе.
- Промерить рентгенограмму и определить углы θ, пользуясь формулой (9).
- Вычислить по формуле (6) межплоскостные расстояния dhkl для всех линий рентгенограммы (как для α, так и β). Найденные значения dhkl выписать в порядке убывания и сравнить с данными таблиц межплоскостных расстояний различных веществ. Определить исследуемое вещество.
- Выписать индексы (hkl) всех отражений и рассчитать из dhkl значения периодов элементарной ячейки ahkl по формуле (13). Построить зависимость y(x): y = ahkl, x = cos2θ.
- Аппроксимировать функцию y(x) полиномом первой степени:
y(x) = y0 + k0x (16)
используя для этих целей MathCad или электронные таблицы Excel. Найти истинное значение периода элементарной ячейки a = y0 и коэффициент k0. Рассчитать по формуле (16) значения y(x) и найти среднеквадратичную ошибку в определении периода элементарной ячейки Δa по формуле (17).Δa =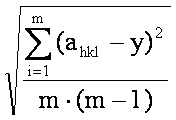 (17)
(17)
Здесь m - число отражений - Используя формулы (14), (15), рассчитать плотность материала ρ, зная число базисных атомов N, и рассчитать число атомов в ячейке N, зная плотность материала ρ.
Подготовить письменный отчет по работе. К отчету приложить рабочие рентгенограммы. В отчете должны быть сформулированы цель работы и основные положения теории. Все необходимые расчеты должны быть оформлены в виде таблицы. При составлении таблицы пронумеровать все линии в порядке возрастания углов θ и оценить их интенсивность I по пятибалльной системе: очень сильная – О.с., сильная – С., средняя – Ср., слабая – Сл., очень слабая – О.сл..
Результаты расчета рентгенограммы, определения межплоскостных расстояний и периода решетки.
| № линии i | I | 2Li (мм) | θi (грд) | sinθi | α или β | hkl | dhkl эксп. Å | dhkl табл. Å | Δ dhkl Å | ahkl Å | x = cos2θi | y | (ahkl–y)2 |
| 1 | |||||||||||||
| 2 | |||||||||||||
| 3 | |||||||||||||
| ... | |||||||||||||
| a±Δa= , V= , ρ= | |||||||||||||
В конце отчета необходимо сформулировать выводы.
- Горелик С. С., Расторгуев Л. Н., Скаков Ю. А. Рентгенографический и электронографический анализ. М.: Металлургия, 1971. С. 7 -25, 54 - 69.
- Пинес Б. Я. Лекции по рентгеноструктурному анализу. Харьков: Изд-во ХГУ, 1967. С. 255 - 265.
- Уманский Я. С. Рентгенография металлов. М.: Металлургия, 1967. С. 7 - 27, 52 - 61, 168 - 176.
- Миркин Л. И. Справочник по рентгеноструктурному анализу поликристаллов. М.: ГИФМЛ. 1961.
- Кристаллография, рентгенография и электронная микроскопия./ Под ред. Уманского Я. С. и др. М.: Металлургия, 1982.