Глава 2.12

Распределение вдоль инверсионного канала квазиуровня Ферми

Предыдущий анализ позволяет получить распределение вдоль инверсионного канала квазиуровня Ферми    , его градиента    и заряда свободных носителей Q_n(у). За основу возьмем выражение для полного тока в канале в виде (2.8.5). Будем считать, что подвижность    не меняется вдоль инверсионного канала. Из условия непрерывности тока следует, что произведение

(2.12.1)

должно оставаться величиной постоянной вдоль инверсионного канала. Заметим, что при больших величинах напряжения исток-сток V_DS допущение о постоянстве подвижности   = const может не выполняться. Физически зависимость подвижности    от положения вдоль канала может быть обусловлена ее зависимостью от концентрации свободных носителей. Поэтому в дальнейшем будем считать напряжение исток-сток V_DS малым, когда   = const. Для области слабой и сильной инверсий соотношения (2.9.10), (2.10.9), (2.9.11) и (2.10.11) дают соответственно

;

(2.12.2)

;

(2.12.3)

где Q_n0 - заряд электронов в канале при   = 0 (или вблизи истока, или при равновесных условиях).

Проведем интегрирование уравнения (2.12.1) с учетом (2.12.2) и (2.12.3) и с граничными условиями y=0; y = L;   = V_DS  ;   = 0.

Предполагается, что длина канала L  много больше области изменения легирующей концентрации вблизи стока и истока.

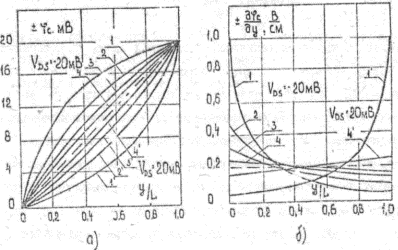
Рис. 2.12.1. Распределение а) квазиуровня Ферми    и   б) градиента квазиуровня Ферми     вдоль инверсионного канала.

1,1' - m/n =1; 2,2' - m/n = 0,5; T=80K
3,3' - m/n = 1; 4,4' - m/n = 0,5; T=290K

Пунктирная линия соответствует линейному распределению квазиуровня Ферми    вдоль канала.

Получаем выражения для распределения квазиуровня Ферми вдоль канала в области слабой инверсии

.

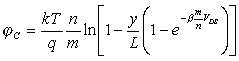(2.12.4)

Для градиента квазиуровня получаем после дифференцирования (2.12.4)

.

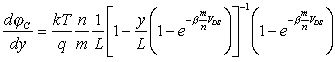(2.12.5)

Поскольку вдоль инверсионного канала произведение (2.12.1) остается постоянным, то, следовательно, заряд свободных электронов Q_n линейно спадает вдоль канала, как вытекает из (2.12.5)

.

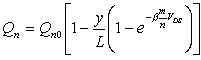(2.12.6)

Ha рис.2.12.1 приведены величины квазиуровня и его градиента    как функция координаты вдоль канала у в области слабой инверсии.

Для области сильной инверсии (2.12.1) с учётом (2.12.3) и (2.12.4) дает

;

;

;

(2.12.7)

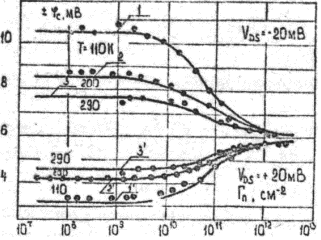
Рис. 2.12.2. Зависимость квазиуровня Ферми    в точке канала y/L=0,3 в зависимости от избытка электронов Г_n  при равных температурах Т и напряжениях V_DS . Точки - эксперимент, сплошная линия - расчет.

Следовательно, в области сильной инверсии квазиуровень Ферми    линейно меняется вдоль канала, заряд электронов постоянен в каждой точке канала. Отметим, что соотношения (2.9.11), (2.10.11), являющиеся основой (2.12.3), справедливы в области сильной инверсии, когда    . Численный расчет уравнения (2.12.1) для всего реально изменяющегося диапазона поверхностных избытков Г_n приведен на рис. 2.12.2. Из рис. 2.12.2 следует, что в области избытков Г_n << 10⁹см^-2 справедливы соотношения (2.12.5 - 2.12.6), а в области Г_n > 10¹²см^-2 - соотношения (2.12.7). В промежуточной области необходим численный расчет.