5.4.1. Дисперсионные кривые для двухатомной одномерной цепочки
Построим дисперсионные кривые для оптических ![]() и акустических
и акустических ![]() колебаний двухатомной
одномерной цепочки атомов.
колебаний двухатомной
одномерной цепочки атомов.
При малых значениях волнового числа ±
k значения ![]() возрастают
пропорционально модулю волнового числа
возрастают
пропорционально модулю волнового числа ![]() .
.
Пользуясь уравнением
(5.41) легко установить, что максимальное значение частоты для акустической
ветви колебаний достигается при ![]() ,
т. е. на границе зоны Бриллюэна, где
,
т. е. на границе зоны Бриллюэна, где ![]() . Это значение равно
. Это значение равно 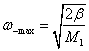 . При этом групповая скорость обращается в нуль
. При этом групповая скорость обращается в нуль ![]() . Таким образом, поведение дисперсионной кривой
. Таким образом, поведение дисперсионной кривой ![]() полностью аналогично
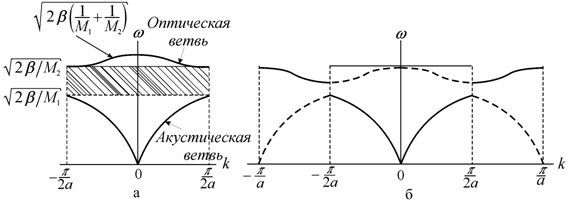
таковому для моноатомной цепочки, рассмотренной выше, и описывается нижней (акустической) ветвью (рис. 5.10, а).
полностью аналогично
таковому для моноатомной цепочки, рассмотренной выше, и описывается нижней (акустической) ветвью (рис. 5.10, а).
Для
оптической ветви при значениях
волновых чисел k, близких к нулю частота имеет максимальное значение, равное 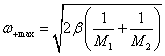 . С ростом волнового числа значение
. С ростом волнового числа значение ![]() уменьшается (рис.
5.10, а), достигая при
уменьшается (рис.
5.10, а), достигая при ![]() своего минимального значения
своего минимального значения 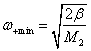 . При
. При ![]() фазовая скорость
оптических колебаний
фазовая скорость
оптических колебаний ![]() стремится к
бесконечности, а групповая
стремится к
бесконечности, а групповая ![]()
![]() равна нулю.
равна нулю.
Таким образом, весь спектр разрешенных частот для цепочки, состоящей из чередующихся атомов двух сортов с массами M1 и M2 (причем M1>M2), заключен в интервалах
·
от 0 до ![]() для
для ![]() акустических частот;
акустических частот;
·
от ![]() до
до 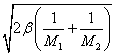 для
для ![]() оптических частот.
оптических частот.
Между
этими интервалами расположена полоса запрещенных частот в пределах от ![]() до
до ![]() (рис. 5.10).
(рис. 5.10).
|
|
|
Рис. 5.10. Дисперсионные кривые для двухатомной линейной цепочки в
случаях: а − приведенной зоны Бриллюэна (полоса запрещенных частот
выделена штриховкой); б − расширенной зоны Бриллюэна [65] |
При большой разнице в массах атомов в цепочке (M1 >> M2) интервал частот оптических колебаний очень узок. Все частоты оптических колебаний в этом случае близки к предельному значению частоты
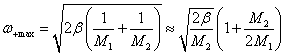 ,
,
что следует из разложения подкоренного выражения в ряд и пренебрежения всеми слагаемыми со степенью выше 1:
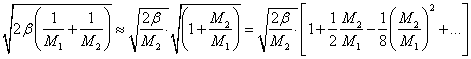 .
.
Дискретный набор длин волн L,
распространяющихся в цепочке, состоящей из чередующихся атомов двух сортов,
может быть найден из условий цикличности ![]()
При этом должно выполняться равенство
![]() что имеет место, когда
что имеет место, когда ![]() .
Последнее приводит к выражению
.
Последнее приводит к выражению ![]() ,
где n − целое число.
,
где n − целое число.
Отсюда
|
|
(5.50) |
Из условия (5.50) можно найти интервал длин волн L. При ![]() значение максимальной
длины волны, способной распространяться в рассматриваемой цепочке, будет равно
длине этой цепочки:
значение максимальной
длины волны, способной распространяться в рассматриваемой цепочке, будет равно
длине этой цепочки: ![]() . Минимальная длина волны при
. Минимальная длина волны при ![]() будет
будет ![]() . Следовательно, минимальная длина волны
. Следовательно, минимальная длина волны ![]() , распространяющейся в цепочке из атомов двух сортов, вдвое больше,
чем в моноатомной цепочке. Число различных длин волн L в каждой ветви спектра определяется числом дискретных значений
волнового числа k, расположенных в
интервале от
, распространяющейся в цепочке из атомов двух сортов, вдвое больше,
чем в моноатомной цепочке. Число различных длин волн L в каждой ветви спектра определяется числом дискретных значений
волнового числа k, расположенных в
интервале от ![]() до
до ![]() , и равно
, и равно ![]() .
Поскольку ветвей колебаний в рассматриваемом случае две, то полное число
различных состояний, соответствующих акустической и оптической ветвям спектра,
как и в случае моноатомной цепочки, равно N
– полному числу атомов в цепочке.
.
Поскольку ветвей колебаний в рассматриваемом случае две, то полное число
различных состояний, соответствующих акустической и оптической ветвям спектра,
как и в случае моноатомной цепочки, равно N
– полному числу атомов в цепочке.
Дискретный
(или, точнее, квазидискретный, поскольку расстояния между соседними значениями
частот очень малы) спектр частот ![]() определяется набором
модулей волновых чисел, заключенных в пределах от
определяется набором
модулей волновых чисел, заключенных в пределах от ![]() до
до ![]() , внутри которых находится первая зона Бриллюэна для
двухатомной цепочки.
, внутри которых находится первая зона Бриллюэна для
двухатомной цепочки.
В
обеих ветвях колебаний каждому значению частоты ![]() соответствуют две
волны с волновыми числами
соответствуют две
волны с волновыми числами ![]() и
и ![]() , поэтому зависимость
, поэтому зависимость ![]() обычно представляется
кривыми, расположенными симметрично относительно оси
обычно представляется
кривыми, расположенными симметрично относительно оси ![]() в зоне Бриллюэна и
называется приведенной зоной Бриллюэна
(рис. 5.10, а). Вместе с тем, период решетки, равный в данном случае 2a определяет
период функции
в зоне Бриллюэна и
называется приведенной зоной Бриллюэна
(рис. 5.10, а). Вместе с тем, период решетки, равный в данном случае 2a определяет
период функции ![]() , равный размерам зоны Бриллюэна:
, равный размерам зоны Бриллюэна: ![]() . Это позволяет транслировать кривую
. Это позволяет транслировать кривую ![]() по оси k на произвольное число
периодов
по оси k на произвольное число
периодов ![]() , и строить расширенную
зону Бриллюэна (рис. 5.10, б).
, и строить расширенную
зону Бриллюэна (рис. 5.10, б).
Рассмотрим,
как меняется характер акустических ![]() и оптических
и оптических ![]() колебаний при приближении к границе зоны Бриллюэна
колебаний при приближении к границе зоны Бриллюэна ![]() . Вблизи этой границы (т. е. при
. Вблизи этой границы (т. е. при ![]() , где
, где ![]() ) отношения амплитуд колебаний тяжелых и легких атомов имеют
вид: для акустической ветви
) отношения амплитуд колебаний тяжелых и легких атомов имеют
вид: для акустической ветви
|
|
(5.51) |
для оптической ветви
|
|
(5.52) |
Выражения
(5.51) и (5.52) показывают, что по мере приближения к границе зоны Бриллюэна
(т. е. при ![]() ) происходит уменьшение амплитуды
) происходит уменьшение амплитуды ![]() колебаний легких атомов
в акустической ветви и амплитуды
колебаний легких атомов
в акустической ветви и амплитуды ![]() колебаний тяжелых
атомов − в оптической. При этом, как и при малых значениях волнового
числа k, в акустической ветви соседние атомы колеблются в фазе, а в
оптической − в противофазе.
колебаний тяжелых
атомов − в оптической. При этом, как и при малых значениях волнового
числа k, в акустической ветви соседние атомы колеблются в фазе, а в
оптической − в противофазе.
При
переходе от цепочки, состоящей из атомов двух сортов, к моноатомной цепочке ![]() область запрещенных
частот между ветвями
область запрещенных
частот между ветвями ![]() и
и ![]() исчезает. При этом
оптические ветви в интервалах
исчезает. При этом
оптические ветви в интервалах ![]() и
и ![]() переходят в
акустические ветви в интервалах
переходят в
акустические ветви в интервалах ![]() и
и ![]() соответственно. Так
как при этом меняется период трансляции, исчезают оптические ветви в интервале
соответственно. Так
как при этом меняется период трансляции, исчезают оптические ветви в интервале ![]() и акустические ветви в
интервалах
и акустические ветви в
интервалах ![]() и
и ![]() . Таким образом, при сближении масс атомов в цепочке спектр
акустических и оптических колебаний вырождается в две акустические ветви (рис.
5.5).
. Таким образом, при сближении масс атомов в цепочке спектр
акустических и оптических колебаний вырождается в две акустические ветви (рис.
5.5).