5.4. Колебательный спектр двухатомной одномерной цепочки. Акустическая и оптическая ветви колебаний
Рассмотрим продольные колебания атомов одномерной решетки с базисом, когда на одномерную элементарную ячейку Бравэ с параметром 2a приходится два атома разных сортов, массы которых обозначим M1 и M2 (рис. 5.8). Силы, действующие между парами различных атомов, одинаковы [59]. Пусть вдоль прямой линии располагается N ячеек. Система обладает 2N степенями свободы.
|
|
|
Рис. 5.8.
Двухатомная линейная цепочка |
Обозначим 2n четное положение равновесия атомов с массой M1, а 2n+1– нечетное для атомов с массой M2.
Пусть 
– смещение атомов с массой M1 вдоль направления x
в момент времени t относительно его
положения равновесия. Соответственно 
– смещение атома с
массой M2 из его положения
равновесия. Пусть (вновь, как и для моноатомной цепи) смещения малы
относительно межатомного расстояния a,
а силы взаимодействия квазиупругие. Будем учитывать взаимодействие только
соседних атомов. Тогда на выбранные атомы будут действовать силы
|
|
(5.34) |
,
.Воспользуемся вторым законом Ньютона для записи уравнения движения атомов обоих типов:
|
|
(5.35) |
,
.Учтем, что колебания атомов разных масс могут происходить с разными
амплитудами 
и 
. Решение системы уравнений (5.35) будем искать в виде
бегущих волн:
|
|
(5.36) |
,
.Подставим эти решения в уравнения (5.35) и сократим общий множитель 
в каждом из
уравнений. Получим систему уравнений относительно амплитуд смещений и .
|
|
(5.37) |
.Ненулевым значениям амплитуд и соответствует обращение в нуль определителя из
коэффициентов системы уравнений (5.37).
|
|
(5.38) |
и
|
|
(5.39) |
Отсюда получим уравнение, связывающее частоту колебаний w и волновое число k:
|
|
(5.40) |
Корни этого биквадратного уравнения
|
|
(5.41) |
.Уравнение (5.41) также можно записать как
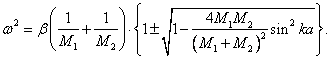
Частота колебаний w не может быть отрицательной величиной,
поэтому далее рассматриваются только положительные значения. Из формулы (5.41)
следует, что каждому волновому числу k
соответствуют два значения частоты w, а значит две различные ветви спектра
частот 
и 
(моды колебаний), причем как частоты 
, так и частоты 
не зависят от номера
атома в цепочке n. Итак, эти частоты являются частотами собственных колебаний
любого из атомов цепочки.
Рассмотрим поведение ветвей частот и в зависимости от
волнового числа k.
При малых волновых числах k
(вблизи центра зоны Бриллюэна), т. е. когда ka<< 1 справедливо приближенное равенство
. Подставляя этот результат в уравнение (5.41), получим
|
|
(5.42) |
.При 
для ветви частот получим
|
|
(5.43) |
,поскольку в этом случае вторым слагаемым под корнем в уравнении (5.42) можно пренебречь.
Рассмотрим ветвь колебаний . В этом случае вторым слагаемым под корнем в уравнении
(5.42) пренебречь нельзя. Обозначим 
и разложим 
в ряд, ограничиваясь
двумя первыми слагаемыми разложения
Тогда в силу малости членов более высокого порядка по x, получим для выражение
|
|
(5.44) |
.Таким образом, при малых значениях волнового числа частоты колебаний и записываются в виде:
|
|
(5.45) |
,
.Если принять, что массы колеблющихся атомов одинаковы (
), то в этом случае выражение совпадает с частотой
колебаний цепочки из одинаковых атомов. Значение скорости звука для этой ветви
|
|
(5.46) |
.Наряду с в одномерной цепочке
атомов двух сортов, в отличие от одномерной моноатомной цепочкой, присутствует
дополнительная ветвь колебаний. При малых
значениях волнового числа k частоты
колебаний определяются величиной
коэффициента квазиупругой силы b
и приведенной массой атомов цепочки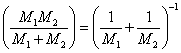 
.
Чтобы выяснить физический смысл 
ветви, сопоставим
значения амплитуд колебаний ветвей и при малых значениях
волнового числа k.
Подставим формулу (5.45) для в (5.37):
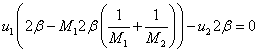
и найдем
отношение амплитуд смещений атомов разного сорта:
|
|
(5.47) |
.Из уравнения (5.47) следует, что при малых волновых числах k амплитуды смещений обратно пропорциональны массам атомов, а знак «-» показывает, что соседние атомы (т. е. атомы разного сорта) колеблются в противофазе (рис. 5.9).
|
|
|
Рис. 5.9.
При малых значениях волнового числа k атомы разного сорта колеблются в
противофазе |
Центр масс системы имеет амплитуду смещений 
(т. к. из
формулы (5.47) следует, что 
). Следовательно, центр масс системы при колебаниях с
частотами остается фиксированным. Подобные колебания могут быть,
например, возбуждены в ионных кристаллах электрическим полем световой волны. Поэтому
ветвь колебаний
получила название оптической.
Подстановка из (5.45) в (5.37)
приводит к выражению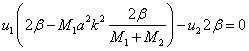 
, и отношение амплитуд смещений атомов разного сорта в
этом случае имеет вид
|
|
(5.48) |
.Вблизи центра зоны Бриллюэна (при k®0) знаменатель в правой части выражения (5.48) стремится к единице, и отношение амплитуд также становится равным единице:
|
|
(5.49) |
.Равенство (5.49) показывает, что в данном случае колебания происходят в
фазе и имеют приблизительно одинаковые амплитуды. Это характерно для
акустической волны, что и было причиной названия ветви колебаний акустической ветвью.
Таким образом, характер колебаний атомов в двухатомной одномерной цепочке оказывается значительно более сложным, чем в моноатомной.
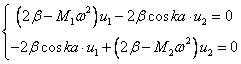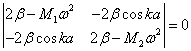
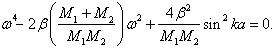
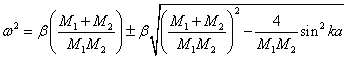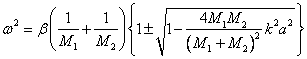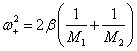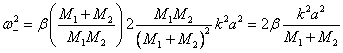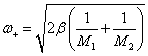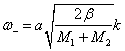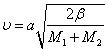