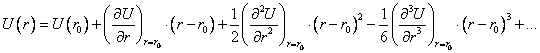5.2. Гармоническое приближение

Перейдем от рассмотрения колебаний в модели непрерывной однородной среды, к колебаниям системы дискретных частиц. Такой системой является кристаллическая решетка.

Модель неподвижных атомов в кристалле противоречит основным постулатам квантовой теории. В частности, она противоречит принципу неопределенности Гейзенберга, который заключается в том, что если точно определена координата частицы, то импульс ее не определен, и наоборот [57, 64]. В математическом представлении этот принцип в случае одномерного движения частицы выглядит так:

.

(5.9)

Соотношение (5.9) означает, что квантовая частица не может находиться в покое ( p_x=0; Dp_x=0) в определенном месте пространства (Dx=0). Локализация частицы в какой-либо точке означает определенность ее координаты (Dx®0), что должно привести к росту неопределенности ее импульса Dp_x и, соответственно, кинетической энергии , что является энергически невыгодным. Кроме того, увеличение Dx приведет к росту потенциальной энергии (b − коэффициент квазиупругой силы), что также является невыгодным.

Будем исходить из зависимости потенциальной энергии взаимодействия атомов от межатомного расстояния (рис. 2.1), характер которой обусловлен совокупностью ион−ионных, ион−электронных и электрон−электронных взаимодействий, определяющих силы межатомного взаимодействия. Минимум кривой отвечает балансу сил притяжения и отталкивания и имеет место при , что отвечает равновесному расстоянию между частицами. При , как видно из рис. 2.3, преобладают силы отталкивания, а при  - силы притяжения. Силы, действующие на атом, связаны с потенциальной энергией межатомного взаимодействия соотношением

,

(5.10)

где  − радиус-вектор, связывающий атом в начале координат с взаимодействующим с ним соседним атомом.

Таким образом, при  производная энергии  и сила взаимодействия  направлена так же, как и радиус-вектор . При  производная  и направление силы  противоположно направлению вектора . И, наконец, при  производная  и .

Для малых отклонений от точки равновесия, как было показано в главе 2, потенциальную энергию системы взаимодействующих атомов U(r) можно разложить в ряд Тейлора вблизи точки .

(5.11)

Из кривой зависимости потенциальной энергии от расстояния между атомами (рис. 2.2) следует, что первая производная , а вторая производная 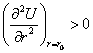. Если, как чаще и бывает, вблизи точки  силы отталкивания меняются быстрее, чем силы притяжения, то третья производная .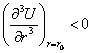

Обозначим в формуле (5.11) , , 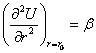, а смещение из положения равновесия , тогда

.

(5.12)

В результате сила, действующая на атом при его движении вдоль оси,

.

(5.13)

В гармоническом приближении ограничиваются линейной зависимостью силы от смещения

.

(5.14)

Формула (5.14) отвечает закону Гука, поэтому при рассмотрении колебаний атомов в гармоническом приближении силу F называют квазиупругой.

Колебания под действием возвращающей силы, пропорциональной смещению, называют гармоническими колебаниями.

Итак, основные положения гармонического приближения заключаются в следующем:

• средние равновесные расстояния между соседними атомами отвечают минимуму кривой потенциальной энергии U(r) и соответствуют статистической модели кристалла;
• атомы колеблются относительно средних положений своих центров тяжести, причем если амплитуды колебаний достаточно малы, то можно ограничиться учетом только квадратичного члена в разложении (5.11).

Гармоническая модель согласуется со многими экспериментальными данными. Однако некоторые свойства кристаллов, например тепловое расширение, могут быть объяснены лишь при учете кубического слагаемого в выражении для энергии (5.11). Такое приближение называют ангармоническим.