5.1. Одномерные колебания однородной струны

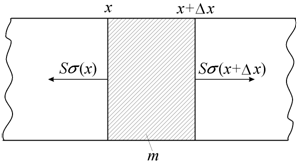
Рассмотрим однородную бесконечную струну с линейной плотностью r, вдоль которой может распространяться продольная волна [59]. Обозначим s нормальные упругие напряжения, возникающие в струне. Тогда на элемент струны длиной Dx и площадью поперечного сечения S (рис. 5.1) действуют силы: Ss(x) слева и Ss(x+Dx) справа. Результирующая сила, действующая на этот элемент струны, будет

	(5.1)
Рис. 5.1. К выводу уравнения распространения упругих волн в однородной струне

 

Результат действия силы F заключается в смещении центра масс элемента Dx, которое обозначим u(x,t). Тогда, приняв  массу элемента, где  − плотность материала струны, в соответствии со вторым законом Ньютона можно записать уравнение движения

,

(5.2)

где  − ускорение.

Поделив обе части уравнения (5.2) на Dx и, приняв условие малости  этого элемента Dx®0, получим

.

(5.3)

Как было показано в главе 4, закон Гука для изотропных твердых тел имеет вид

,

(5.4)

где E − модуль Юнга, (отношение силы F, действующей на тело, к величине относительного удлинения ), а e  − деформация. Поскольку , то можно записать

.

(5.5)

Окончательно уравнение движения для смещения u(x,t) примет вид

.

(5.6)

Уравнение (5.6) соответствует упругой волне, распространяющейся вдоль однородной струны. Решение этого уравнения можно найти в виде продольной монохроматической волны

,

(5.7)

где  − амплитуда колебаний, k − волновое число, равное  (l − длина волны), w − циклическая частота колебаний, t − время.

Найдем зависимость частоты от волнового числа, подставив решение (5.7) в уравнение движения (5.6).

,

(5.8)

где u − скорость распространения волны вдоль струны.

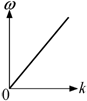
Из формулы (5.8) следует, что для упругой волны, распространяющейся вдоль бесконечной однородной упругой струны, частота колебаний линейно зависит от волнового числа (рис. 5.2).

 

Рис. 5.2. Зависимость частоты колебаний непрерывной однородной струны от волнового числа

 

Скорость распространения волны  для данного материала струны величина постоянная, поскольку модуль упругости E и плотность r характеризуют конкретный материал. Например, в железной струне с E = 2,1×10¹¹ Па и r = 7,8×10³ кг/м³ скорость волны составит значение u = 5×10³ м/с.