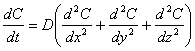3.4.2. Законы Фика

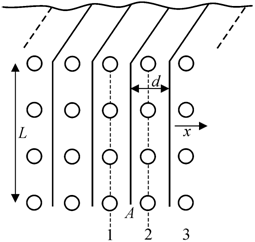
Проведем оценку скорости диффузии множества атомов через определенную плоскость решетки. В качестве модели такого движения рассмотрим движение атомов в простой кубической решетке (рис. 3.39) [78]. Выделим две соседние атомные плоскости, например 1 и 2. Мысленно разделим кристалл на тонкие слои с поперечным сечением и толщиной d. Пусть некоторое количество атомов в каждой плоскости приходится на долю примеси, например в плоскости 1 и в плоскости 2 (такой примесью может быть мышьяк в германии). В процессе диффузии атомы движутся через плоскость А в обоих направлениях. В зависимости от определенных условий результирующий поток атомов направлен либо в одну, либо в другую сторону. Этот результирующий поток и требуется рассчитать.

Рис. 3.39. Геометрическая схема диффузии в объеме простого кубического кристалла

Введем несколько допущений, а также две новые переменные и – объемные концентрации атомов примесей в плоскостях 1 и 2. Тогда и , где – объем выделенного атомного слоя. Каждый атом примеси совершает в среднем один прыжок за секунд. Допустим, что атомы могут с одинаковой вероятностью совершать прыжки либо вправо, либо влево. После одного прыжка атом, находившийся прежде в плоскости 2, перейдет либо в плоскость 1, либо в плоскость 3. Если каждый атом примеси совершит только один прыжок, то половина атомов из числа , находившихся в плоскости 1, переместится в одном направлении. Следовательно, за период времени плоскость А слева направо пересечет атомов. Аналогично за тот же период времени атомов пройдет через плоскость справа налево. Результирующее количество атомов примеси , проходящих за 1 секунду через плоскость А, точно равно разности между этими двумя потоками.

,

(3.41)

где dN обозначает результирующее количество атомов, движущихся в направлении слева направо, а . Концентрации и можно связать друг с другом через градиент концентрации . Тогда , следовательно, или . Опять примем , тогда

.

(3.42)

Левая часть уравнения (3.41) представляет собой результирующее количество атомов, проходящих в секунду через единицу поперечного сечения плоскости А. Эта величина называется плотностью потока диффундирующих атомов. Постоянная D выражается точно таким же соотношением, как и при анализе одномерного движения атомов (уравнение 3.38).

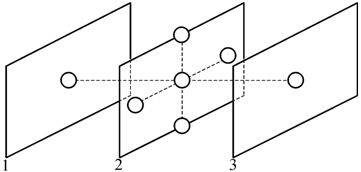
Учтем теперь то, что диффундирующие атомы могут двигаться в трех направлениях. Рассмотрим простую кубическую структуру. Каждый атом может поменяться местами с любым из своих шести ближайших соседей (рис. 3.40), но только один из шести прыжков переведет атом из плоскости 2 в плоскость 1.

Рис. 3.40. Геометрическая схема обмена мест с шестью ближайшими соседями
в простой кубической решетке

Следовательно, уравнение (3.42) преобразуется к виду

(3.43)

и

,

(3.44)

где .

Обозначим плотность потока диффундирующих атомов , тогда уравнение (3.44) можно представить в виде

или, для трехмерного случая, .

(3.45)

Выражение (3.45) широко известно как первый закон Фика для диффузии в изотропной среде. В общем случае диффузия анизотропна, поэтому коэффициент диффузии D зависит от направления и представляет собой тензор второго ранга.

Второй закон Фика учитывает то, что поток атомов в процессе диффузии может меняться, т. е. принимает во внимание нестационарность потока. При этом скорость накопления диффундирующего вещества в данном объеме является разностью между входящим и выходящим потоками за единичное время. Для двух параллельных плоскостей, площадь каждой из которых равна единице, а расстояние между ними dx, поток через первую плоскость будет соответствовать выражению (3.45), а через вторую −

.

(3.46)

Разность этих двух потоков составляет

.

(3.47)

При условии не зависящего от концентрации коэффициента диффузии получим второй закон Фика для одномерной диффузии в дифференциальной форме:

.

(3.48)

Концентрация C здесь зависит от времени t и от глубины диффузии x.

Для диффузии в трех измерениях второй закон Фика принимает вид

.

(3.49)

Большинство экспериментальных методов измерения коэффициента диффузии D основано на создании условий, близких к макроскопическому одномерному перемещению атомов. Расчет коэффициента диффузии D по экспериментальным данным проводится с помощью закона Фика или одной из его модификаций. Типичный эксперимент состоит в нанесении слоя радиоактивных атомов (путем выпаривания раствора или гальваническим покрытием) на чистую плоскую поверхность твердого тела, для которого требуется определить коэффициент диффузии. Затем твердое тело нагревается до температуры, при которой нужно определить коэффициент диффузии D, и выдерживается в этих условиях в течение времени t, достаточно длительного для диффузии радиоактивных атомов на заметную глубину (чтобы среднеквадратичное значение X было, например, порядка 0,5 мм). Потом измеряется концентрация радиоактивных атомов на различном расстоянии вглубь от поверхности твердого тела. Эти измерения основаны на определении радиоактивности тонких слоев твердого тела, которые сошлифовываются с помощью какого-нибудь механического приспособления.

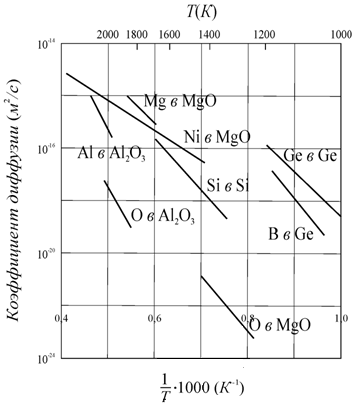
Ниже приведены данные о типах кристаллических решеток, коэффициентах диффузии и энергиях активации диффузии для некоторых металлов (табл. 3.2) и неметаллов (табл. 3.3) [98], а на рис. 3.41 показаны полученные экспериментально температурные зависимости коэффициентов диффузии некоторых неметаллических систем.

Таблица 3.2

Диффузионные характеристики для металлических систем

Растворенное вещество	Растворитель	D0 (м^2/с)	Q (кДж/моль)
Углерод	ГЦК железо		142
Углерод	ОЦК железо		122
Железо	ГЦК железо		268
Железо	ОЦК железо		240
Никель	ГЦК железо		280
Магний	ГЦК железо		282
Цинк	Медь		191
Медь	Алюминий		126
Медь	Медь		197
Серебро	Серебро		184
Углерод	Гексагональный титан		182

Таблица 3.3

Диффузионные характеристики для неметаллических систем

Растворенное вещество	Растворитель	D0 (м^2/с)	Q (кДж/моль)
Al	Al2O3		477
O	Al2O3		636
Mg	MgO		330
O	MgO		344
Ni	MgO		202
Si	Si		460
Ge	Ge		291
B	Ge		439

Рис. 3.41. Температурные зависимости коэффициентов диффузии для некоторых неметаллических систем [98]

Назад Далее...