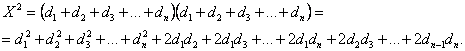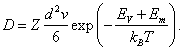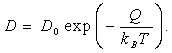3.4.1. Диффузия в кристаллах
Некоторые общие кристаллографические особенности процесса диффузии вполне очевидны, если принять во внимание геометрию кристалла. Прежде всего, диффузия почти всегда осуществляется постепенно, причем длина элементарных «шагов» порядка одного атомного диаметра, т. е. несколько ангстрем. Атомы движутся прыжками из одного положения в решетке в другое. В сумме эти элементарные прыжки обеспечивают перемещение атомов на большие расстояния.
Выясним, каков механизм отдельных атомных прыжков. Существует несколько возможных схем: движение вакансий, движение атомов внедрения или какой-либо способ взаимного обмена местами между атомами (рис. 3.34).
|
|
|
Рис. 3.34. Атомные перемещения, которые приводят к
диффузии: |
Задача сводится к тому, чтобы оценить относительный вклад каждого из этих механизмов в общий диффузионный процесс, происходящий в данной системе при определенной температуре.
Диффузия за счет перемещения вакансий происходит в тех случаях, когда вакансии решетки обмениваются местами с соседними атомами. Последовательность актов, за счет которых вакансия движется по решетке, показана на рис. 3.34, а. Этот процесс зависит от двух факторов: образования вакансий в решетке и их последовательного перемещения. Диффузия атомов внедрения также является двухступенчатым процессом. Сначала атом, находившийся в узле решетки, перескакивает в междоузлие: из положения 1 в положение 2 (рис. 3.34, б), после чего происходят последовательные перескоки этого атома в ближайшие междоузлия 2 – 3 – 4 – 5 – 6 и т. д.
Диффузия путем обмена мест может осуществляться несколькими различными способами. Так, возможен одновременный обмен местами двух, трех, четырех или большего числа атомов. На рис. 3.34, в и г показаны обмены местами между двумя и четырьмя атомами в кубической решетке соответственно.
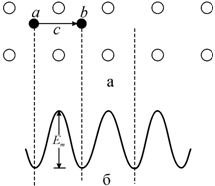
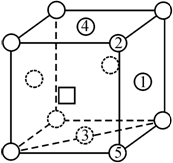
Скорость диффузии атомов небольшого размера по междоузлиям сплава определяется энергией, необходимой для передвижения атомов внедрения по кристаллической решетке. Элементарный акт диффузии в таких сплавах схематически показан на рис. 3.35, а. Поскольку в междоузлиях а и b атомы занимают положения равновесия, то эти положения соответствуют минимуму энергии. Кроме того, из условий симметрии следует, что максимум энергии достигается, когда атом из положения a смещается в точку с, находящуюся посередине между положениями равновесия. Зависимость потенциальной энергии атома от его положения показана на рис. 3.35, б.
|
|
|
Рис. 3.35. Диффузия по междоузлиям: |
Увеличение
энергии кристалла ![]() при переходе атома из
положения a в среднее положение с
вызвано главным образом появлением упругих напряжений, возникающих при
«протискивании» диффундирующего атома в узком пространстве между атомами
решетки. Для многих сплавов величина
при переходе атома из
положения a в среднее положение с
вызвано главным образом появлением упругих напряжений, возникающих при
«протискивании» диффундирующего атома в узком пространстве между атомами
решетки. Для многих сплавов величина ![]() составляет около 1 эВ. Поскольку средняя тепловая энергия
атома при умеренных температурах не превышает 0,1 эВ, то для преодоления
энергетического барьера
составляет около 1 эВ. Поскольку средняя тепловая энергия
атома при умеренных температурах не превышает 0,1 эВ, то для преодоления
энергетического барьера ![]() необходима большая
флуктуация энергии. Следовательно, частота прыжков атома из одного междоузлия в
другое определяется частотой появления достаточно больших флуктуаций.
необходима большая
флуктуация энергии. Следовательно, частота прыжков атома из одного междоузлия в
другое определяется частотой появления достаточно больших флуктуаций.
Основную
часть времени энергия атома слишком мала для преодоления барьера. Однако иногда
флуктуация повышает энергию атома до величины ![]() , и тогда атом становится способным преодолеть барьер.
Интервал, в течение которого атом обладает энергией, необходимой для
преодоления барьера, пропорционален
, и тогда атом становится способным преодолеть барьер.
Интервал, в течение которого атом обладает энергией, необходимой для
преодоления барьера, пропорционален 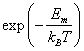 . Поэтому частота прыжков атома в ближайшее междоузлие
решетки по порядку величины составляет
. Поэтому частота прыжков атома в ближайшее междоузлие
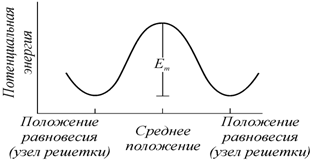
решетки по порядку величины составляет 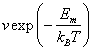 . Поскольку атом может перепрыгнуть в Z
равноценных соседних мест, общая частота прыжков, совершаемых с исходной
позиции, равна
. Поскольку атом может перепрыгнуть в Z
равноценных соседних мест, общая частота прыжков, совершаемых с исходной
позиции, равна
|
|
(3.27) |
Здесь v -
частота тепловых колебаний атома около положения равновесия, имеющая порядок 1013
Гц, Z − количество равноценных
соседних узлов. При диффузии по междоузлиям в кристаллах со структурой ОЦК ![]() , а в кристаллах со структурой ГЦК
, а в кристаллах со структурой ГЦК ![]() . Поскольку величина
. Поскольку величина ![]() экспоненциально
зависит от температуры, то частота прыжков быстро возрастает с увеличением
последней. Например, при диффузии углерода по междоузлиям кристалла железа
величина потенциального барьера
экспоненциально
зависит от температуры, то частота прыжков быстро возрастает с увеличением
последней. Например, при диффузии углерода по междоузлиям кристалла железа
величина потенциального барьера ![]() составляет около 0,9
эВ. Соответственно при комнатной температуре атом углерода совершает примерно
один прыжок за 25 секунд, а при температуре плавления железа (1545 оС)
– до
составляет около 0,9
эВ. Соответственно при комнатной температуре атом углерода совершает примерно
один прыжок за 25 секунд, а при температуре плавления железа (1545 оС)
– до ![]() прыжков в 1 секунду.
прыжков в 1 секунду.
Диффузия
за счет движения вакансий
Теоретические расчеты энергии, необходимой для перемещения атомов с помощью одного из перечисленных выше механизмов, показывают, что в чистых металлах и сплавах со структурой твердых растворов замещения должна преобладать диффузия за счет движения вакансий.
Рассмотрим последовательные этапы этого процесса (рис. 3.36).
Атом 1 в конфигурации, показанной на рис. 3.36, а, может поменяться местами с соседней вакансией в полноупакованной плоской структуре и перейти в положение, показанное на рис. 3.36, в. Оба расположения атомов (а и в) геометрически равноценны, а следовательно, эквивалентны и энергетически. При переходе от конфигурации а к конфигурации в атом 1 должен «протиснуться» между атомами 2 и 3, находящимися в этой же плоскости. В промежуточном положении (рис. 3.36, б) атомы 2 и 3 смещаются с их нормальных положений, и в этом месте решетка будет обладать значительной упругой энергией. Следовательно, промежуточное положение б соответствует более высокому уровню энергии, чем а и в.
|
|
|
Рис. 3.36. Затрудненное движение вакансий в полноупакованной двумерной структуре |
Такому обмену
препятствуют также атомы, которые находятся в соседних атомных плоскостях –
выше и ниже плоскости атомов, показанной на рис. 3.36. Особенно сильно здесь
сказывается влияние двух других атомов, расположенных непосредственно над
местом перехода (один из этих атомов находится в верхней соседней плоскости, а
другой – в нижней). Эти атомы также мешают переходу рассматриваемого атома 1 из
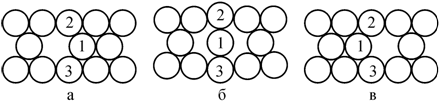
положения а в положение в. Например, расположение атомов вокруг вакансии в ГЦК
решетке (рис. 3.37) таково, что для обмена вакансии (она отмечена квадратом) с
атомом 1 необходимо, чтобы диффундирующий атом «протиснулся» между атомами 2,
3, 4 и 5. Во время этого продвижения диффундирующий атом «давит» на указанные
соседние атомы. График зависимости потенциальной энергии от смещения атома
показан на рис. 3.38, причем высота барьера обозначена по-прежнему символом ![]() .
.
|
|
|
|
Рис. 3.37. При обмене местами между вакансией, находящейся на передней грани, и атомом 1 в ГЦК структуре четыре других атома 2, 3, 4, 5 непосредственно взаимодействуют с диффундирующим атомом, когда он находится в среднем положении [78] |
Рис. 3.38. Зависимость потенциальной энергии диффундирующего атома от его расположения |
При
частоте теплового движения v атом v раз в секунду «ударяется» в барьер. Относительная доля
времени, в течение которого атом обладает энергией, достаточной для преодоления
этого барьера, равна
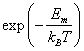 . Однако здесь необходимо учесть дополнительный фактор,
состоящий в том, что ближайшая к атому вакансия существует в данном узле
решетки тоже лишь малую долю времени. Эта доля определяется второй экспонентой
. Однако здесь необходимо учесть дополнительный фактор,
состоящий в том, что ближайшая к атому вакансия существует в данном узле
решетки тоже лишь малую долю времени. Эта доля определяется второй экспонентой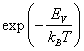 , где
, где ![]() – энергия образования
вакансии. Частота прыжков атома f пропорциональна
произведению этих факторов и по порядку величины равна
– энергия образования
вакансии. Частота прыжков атома f пропорциональна
произведению этих факторов и по порядку величины равна
|
|
(3.28) |
Частота прыжков атома f сильно зависит от температуры. Для таких металлов, как медь, серебро, железо и т. п., обе энергии равны примерно 1 эВ. Поэтому для таких металлов частота прыжков при самодиффузии атомов или диффузии путем замещения гораздо меньше частоты прыжков при диффузии внедренных по междоузлиям примесей. Например, если внедренный в решетку железа атом углерода совершает при комнатной температуре примерно один прыжок за 25 секунд, то атом цинка, заместивший атом меди в ее решетке, также при комнатной температуре совершит только один прыжок в течение тысячи лет.
Перемещение
атомов на большие расстояния
Для решения задачи о перемещении атомов на большие расстояния рассмотрим статистику сложения последовательных прыжков. Рассчитаем смещение атома после того, как он совершил определенное число прыжков. Будем считать, что все прыжки одинаковы по длине и равны межатомному расстоянию, они происходят в решетке с высокой степенью симметрии. Предполагается, что движение атома в различных возможных кристаллографических направлениях совершенно хаотично. Если это так, то нельзя заранее предсказать, по какой траектории будет двигаться отдельный атом после определенного количества прыжков. С достаточной точностью можно определить лишь смещение, усредненное по многим диффундирующим атомам.
Проще всего выполнить такой расчет для случая движения атомов только в одном направлении (вдоль одной прямой). Предположим, что в начальный момент атом находится в точке 0. Далее атом совершает последовательные прыжки длиной d каждый.
Направление каждого прыжка хаотично и не зависит от предыдущих прыжков. Результирующее расстояние X, которое пройдет атом после n прыжков, равно алгебраической сумме всех отдельных прыжков, т. е.
|
|
(3.29) |
где ![]() – длина первого
прыжка,
– длина первого
прыжка, ![]() – второго и т. д.
– второго и т. д.
Очевидно, что расстояние X соответствует произведению длины прыжка d на некоторый множитель n, причем это расстояние
может быть положительным, отрицательным или равным нулю. На самом деле средняя
величина X после множества атомных прыжков в
точности равна нулю, хотя диапазон изменения X лежит в пределах от ![]() до
до ![]() . Равенство этой величины нулю говорит лишь о том, что
положительное направление прыжков не имеет никаких преимуществ перед
отрицательными. Однако существуют другие виды средних значений, которые не
будут равны нулю. К их числу относится, например, среднеквадратичное значение,
которое служит мерой общего (неалгебраического) расстояния, пройденного атомом
от начального положения.
. Равенство этой величины нулю говорит лишь о том, что
положительное направление прыжков не имеет никаких преимуществ перед
отрицательными. Однако существуют другие виды средних значений, которые не
будут равны нулю. К их числу относится, например, среднеквадратичное значение,
которое служит мерой общего (неалгебраического) расстояния, пройденного атомом
от начального положения.
Можно
рассчитать среднее значение ![]() (т. е. среднее из
значений
(т. е. среднее из
значений ![]() для многих атомов,
каждый из которых совершил n прыжков). Для
для многих атомов,
каждый из которых совершил n прыжков). Для ![]() можно написать
следующее выражение:
можно написать
следующее выражение:
|
|
(3.30) |
Среднее
значение ![]() есть сумма средних
величин отдельных слагаемых. Ясно, что каждый квадратичный член равен
есть сумма средних
величин отдельных слагаемых. Ясно, что каждый квадратичный член равен ![]() , т. к.
, т. к. ![]() . Сумма произведений вида
. Сумма произведений вида ![]() после усреднения
движений множества атомов равна нулю, поскольку любая величина
после усреднения
движений множества атомов равна нулю, поскольку любая величина ![]() с равной вероятностью
может быть как положительной, так и отрицательной. Следовательно,
с равной вероятностью
может быть как положительной, так и отрицательной. Следовательно,
|
|
(3.31) |
Соотношение (3. 31) можно переписать в виде
|
|
(3.32) |
Качественная
оценка величины X приводит к выводу, что для того,
чтобы она имела заметную величину, необходимо большое количество прыжков.
Количество прыжков можно выразить как произведение частоты прыжков f и времени t, необходимого для
совершения n атомных прыжков, т. е. ![]() . Тогда выражение (3.32) преобразуется к виду
. Тогда выражение (3.32) преобразуется к виду
|
|
(3.33) |
Параметр ![]() в формуле (3.33)
зависит от свойств материала и от температуры и называется коэффициентом диффузии. Обычно одномерный
коэффициент диффузии D определяется как
в формуле (3.33)
зависит от свойств материала и от температуры и называется коэффициентом диффузии. Обычно одномерный
коэффициент диффузии D определяется как
|
|
(3.34) |
Подстановка (3.34) в уравнение (3.33) дает
|
|
(3.35) |
Видно, что среднеквадратичное расстояние, проходимое диффундирующим атомом, изменяется пропорционально корню квадратному от времени.
В
трехмерном кристалле атомы могут совершать прыжки по все трем направлениям. В
этом случае можно провести аналогичные рассуждения для расчета
среднеквадратичного радиального смещения ![]() в любом направлении от
начальной точки. В итоге получим
в любом направлении от
начальной точки. В итоге получим
|
|
(3.36) |
где f – частота, с которой атом изменяет свое положение в
решетке. В случае кубической симметрии ![]() . Поэтому смещение
. Поэтому смещение ![]() равно
равно
|
|
(3.37) |
Тогда аналогично (3.33) трехмерный коэффициент диффузии определяется как
|
|
(3.38) |
Частота прыжков f в этом уравнении не совпадает с частотой в уравнении (3.34).
Оба уравнения, (3.37) и (3.38), в равной степени применимы для описания диффузии в случаях, которые будут рассмотрены ниже.
Значения
коэффициента диффузии D при данной температуре для
различных твердых тел изменяются в широких пределах. Эти изменения лишь в
слабой степени связаны с изменениями длины скачка d, а почти
целиком обусловлены сильными различиями в значениях частот f. Для
обычных металлов, а также для Ge
и Si коэффициент
диффузии D при комнатной температуре может
принимать широкий диапазон значений – от ![]() до
до ![]() .
.
Чтобы установить зависимость коэффициента диффузии D от температуры, можно использовать выражение (3.28) для частоты f, полученное выше. Тогда для кубических кристаллов получим
|
|
(3.39) |
Все
параметры, стоящие перед экспоненциальным членом, объединяют в коэффициент ![]() , а суммарную энергию
, а суммарную энергию ![]() обозначают Q. Тогда уравнение (3.39) принимает вид
обозначают Q. Тогда уравнение (3.39) принимает вид
|
|
(3.40) |
Величина ![]() часто называется частотным фактором, а Q принято называть энергией
активации процесса диффузии.
часто называется частотным фактором, а Q принято называть энергией
активации процесса диффузии.
Из
уравнения (3.40) следует, что коэффициент диффузии D
экспоненциально зависит от температуры (если действует только единственный
механизм диффузии). Многочисленными экспериментами установлено, что такая
температурная зависимость действительно имеет место для большинства твердых
веществ. Кроме того, из уравнения (3.40) вытекает, что коэффициент ![]() должен быть постоянной
величиной, не зависящей от температуры. По порядку величины
должен быть постоянной
величиной, не зависящей от температуры. По порядку величины ![]() составляет от
составляет от ![]() до
до ![]() . Как показывают экспериментальные данные,
. Как показывают экспериментальные данные, ![]() почти не зависит от
температуры. Однако экспериментальные значения
почти не зависит от
температуры. Однако экспериментальные значения ![]() для многих металлов и
полупроводников, а также для их сплавов несколько превышают
для многих металлов и
полупроводников, а также для их сплавов несколько превышают ![]() .
.
Для ряда
материалов, представляющих практический интерес, энергия активации составляет
от 1 до 4 эВ на атом. Примерно половина величины Q
соответствует энергии образования вакансии ![]() , а другая половина – энергии, соответствующей высоте
потенциального барьера
, а другая половина – энергии, соответствующей высоте
потенциального барьера ![]() . Экспериментальные значения
. Экспериментальные значения ![]() и Q для
некоторых материалов приведены в табл. 3.1
[78].
и Q для
некоторых материалов приведены в табл. 3.1
[78].
Таблица 3.1
Значения диффузионных констант
для некоторых чистых материалов и сплавов
|
Материал |
D0, м2/с |
Q, эВ |
|
Ge в Ge |
7,8∙10-4 |
3,0 |
|
As в Ge |
6,0∙10-4 |
2,5 |
|
Sb в Ge |
1,2∙10-3 |
2,5 |
|
P в Ge |
2,0∙10-4 |
2,5 |
|
Zn в Ge |
4,0∙10-5 |
2,5 |
|
In в Ge |
6,0∙10-6 |
2,5 |
|
Ga в Ge |
5,0∙10-6 |
2,5 |
|
B в Ge |
4,0∙10-4 |
4,5 |
|
Li в Ge |
2,5∙10-7 |
0,5 |
|
Li в Si |
2,3∙10-7 |
0,65 |
|
Cu в Al |
2,3∙10-4 |
1,45 |
|
Th в W |
1,0∙10-4 |
5,4 |
|
Fe в Fe (о.ц.к.) |
1,0∙10-2 |
3,0 |
|
C в Fe (о.ц.к.) |
2,0∙10-5 |
0,9 |
|
Cu в Cu |
2,0∙10-5 |
2,05 |
|
Zn в Cu |
3,4∙10-5 |
1,98 |
|
Cu в латунь с 30% Zn |
3,4∙10-5 |
1,82 |
|
Zn в латунь с 30% Zn |
7,3∙10-5 |
1,77 |
|
Ta в Ta |
2,0∙10-4 |
4,78 |
|
Nb в Nb |
1,3∙10-4 |
4,13 |
|
Fe в Nb |
1,5∙10-4 |
3,38 |
|
Co в Nb |
0,7∙10-4 |
3,06 |
|
U в U |
1,8∙10-7 |
1,20 |

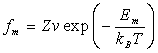
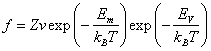 .
.