2.5. Представление об атомных орбиталях
Свойства атомных объектов, а в частности, и поведение электронов в атоме, описывается с помощью аппарата квантовой механики [64]. Одним из основных уравнений квантовой механики является уравнение Шредингера, определяющее изменение состояния квантовой системы с течением времени. В частном виде оно записывается как
|
|
(2.30) |
где ![]() − оператор Гамильтона квантовой системы,
совпадающий с оператором энергии, если он не зависит от времени. Вообще вид
оператора Гамильтона определяется свойствами системы. Для нерелятивистского
движения частицы некоторой массы в потенциальном поле оператор
− оператор Гамильтона квантовой системы,
совпадающий с оператором энергии, если он не зависит от времени. Вообще вид
оператора Гамильтона определяется свойствами системы. Для нерелятивистского
движения частицы некоторой массы в потенциальном поле оператор ![]() действителен и
представляется суммой операторов кинетической и потенциальной энергии частицы. E − полная энергия квантовой
системы, а y − волновая функция
стационарного (не зависящего от времени) состояния системы.
действителен и
представляется суммой операторов кинетической и потенциальной энергии частицы. E − полная энергия квантовой
системы, а y − волновая функция
стационарного (не зависящего от времени) состояния системы.
Волновая
функция y, описывающая
состояния движения микрочастицы, в общем случае является комплексной
однозначной и непрерывной функцией радиус-вектора ![]() от времени t.
от времени t. ![]() удовлетворяет некоторому дифференциальному
уравнению, которое и определяет характер движения частицы.
удовлетворяет некоторому дифференциальному
уравнению, которое и определяет характер движения частицы.
Волновые функции, для которых уравнение (2.31) имеет решения, называются собственными функциями, а соответствующие значения энергии − собственными значениями.
Рассмотрим вопрос об атомных орбиталях на примере простого случая − атома водорода. Решение уравнения Шредингера (2.31) в этом случае имеет вид:
|
|
(2.31) |
где N − постоянная нормировки, определяемая из соотношения ![]() ;
;
![]() − радиальная часть волновой функции;
− радиальная часть волновой функции; ![]() дает вероятность
нахождения электрона на расстоянии r от ядра.
дает вероятность
нахождения электрона на расстоянии r от ядра.
Величина ![]() является собственной
функцией только для целочисленных значений главного
квантового числа
является собственной
функцией только для целочисленных значений главного
квантового числа ![]() . Главное квантовое число n определяет среднее
расстояние электрона от ядра (электронный слой) и, следовательно, его энергию. Орбитальное квантовое число
. Главное квантовое число n определяет среднее
расстояние электрона от ядра (электронный слой) и, следовательно, его энергию. Орбитальное квантовое число ![]() определяет момент
количества движения электрона в атоме и обозначается обычно буквенными
спектроскопическими символами s, p, d, f ( для
определяет момент
количества движения электрона в атоме и обозначается обычно буквенными
спектроскопическими символами s, p, d, f ( для ![]() соответственно).
Угловая часть волновой функции
соответственно).
Угловая часть волновой функции ![]() может быть собственной
функцией только при целочисленных значениях магнитного квантового числа m, находящегося в интервале
может быть собственной
функцией только при целочисленных значениях магнитного квантового числа m, находящегося в интервале ![]() . Магнитное квантовое
число m определяет проекцию момента
количества движения на ось z в
магнитном поле.
. Магнитное квантовое
число m определяет проекцию момента
количества движения на ось z в
магнитном поле.
Собственные
волновые функции атома водорода ![]() называются орбиталями. Типы орбиталей определяются
величиной орбитального квантового числа l и имеют названия,
соответствующие приведенным выше числам s, p, d, f. Для определения орбитали
необходимо указать ее тип (s, p, d, f), значения n и m. При
называются орбиталями. Типы орбиталей определяются
величиной орбитального квантового числа l и имеют названия,
соответствующие приведенным выше числам s, p, d, f. Для определения орбитали
необходимо указать ее тип (s, p, d, f), значения n и m. При ![]() орбитали являются
мнимыми функциями. Удобнее применять действительные орбитали, являющиеся
линейными комбинациями орбиталей nlm. В этом случае
орбитали указываются при помощи значений n и l с
добавлением нижнего индекса, характеризующего тип угловой зависимости, например
орбитали являются
мнимыми функциями. Удобнее применять действительные орбитали, являющиеся
линейными комбинациями орбиталей nlm. В этом случае
орбитали указываются при помощи значений n и l с
добавлением нижнего индекса, характеризующего тип угловой зависимости, например
![]() или
или ![]() .
.
Достаточно
полное представление о свойствах собственной функции (орбитали) атома
водорода дает поверхность,
ограничивающая область пространства, внутри которой содержится 90 % величины ![]() . Часто эту граничную поверхность также называют орбиталью.
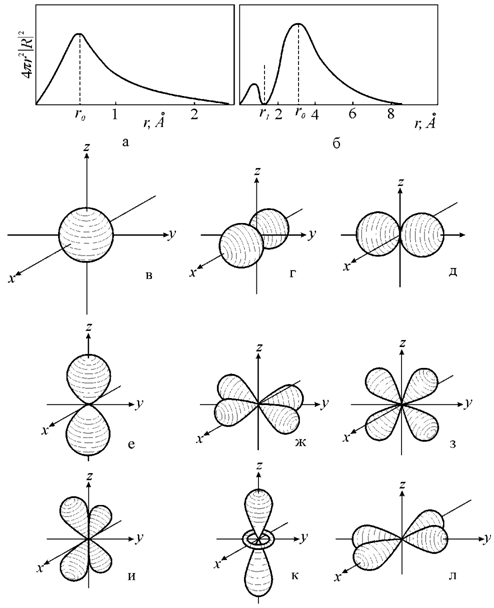
На рис. 2.16 изображены s-, p- и d-орбитали атома
водорода. На этом же рисунке приведены функции R(r).
. Часто эту граничную поверхность также называют орбиталью.
На рис. 2.16 изображены s-, p- и d-орбитали атома
водорода. На этом же рисунке приведены функции R(r).
|
|
|
Рис. 2.16. s-, p- и d-орбитали атома водорода. Изображены граничные поверхности и радиальные
распределения вероятности |
Для полного
описания состояния электрона, помимо трех квантовых чисел n, l, m, необходимо ввести еще и спиновое
квантовое число S, которое может принимать только два значения: ![]() и
и ![]() .
.
Решение уравнения Шредингера для атомов с числом электронов больше единицы весьма сложно, поэтому для описания многоэлектронных атомов используют орбитали атома водорода и тот же набор квантовых чисел n, l, m, S.
При заполнении орбиталей электронами действует правило запрета Паули, согласно которому в каждом квантовом состоянии, характеризующемся определенными значениями квантовых чисел, не может находиться более одного электрона. Два электрона могут занимать одну орбиталь, если у них противоположные спиновые квантовые числа. В соответствии с этим правилом количество электронов, способных разместиться на какой-либо орбитали, строго определено (табл. 2.8).
Таблица 2.8
Характеристики
орбиталей
|
Типы орбитали |
Квантовые числа |
Число орбиталей |
Наибольшее число электронов на орбиталях |
|
s |
|
1 |
2 |
|
p |
|
3 |
6 |
|
d |
|
5 |
10 |
|
f |
|
7 |
14 |
При размещении электронов по эквивалентным орбиталям справедливы так называемые правила Хунда:
• электроны по возможности избегают заполнять одну и ту же орбиталь;
•
при заполнении двух эквивалентных орбиталей двумя
электронами (например, ![]() и
и
![]() ) меньшей энергии соответствует параллельное расположение
спинов.
) меньшей энергии соответствует параллельное расположение
спинов.
Заселение
электронами орбиталей идет в следующей последовательности: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s,
В табл. 2.9 [102] приведены сведения об электронной конфигурации некоторых химических элементов.
Таблица 2.9
Электронная
конфигурация некоторых элементов
|
Элемент |
Символ |
Номер атома |
Электронная конфигурация |
|
Водород |
H |
1 |
|
|
Гелий |
He |
2 |
|
|
Литий |
Li |
3 |
|
|
Бериллий |
Be |
4 |
|
|
Бор |
B |
5 |
|
|
Углерод |
C |
6 |
|
|
Азот |
N |
7 |
|
|
Кислород |
O |
8 |
|
|
Фтор |
F |
9 |
|
|
Неон |
Ne |
10 |
|
|
Натрий |
Na |
11 |
|
|
Магний |
Mg |
12 |
|
|
Алюминий |
Al |
13 |
|
|
Кремний |
Si |
14 |
|
|
Фосфор |
P |
15 |
|
|
Сера |
S |
16 |
|
|
Хлор |
Cl |
17 |
|
|
Аргон |
Ar |
18 |
|
|
Калий |
K |
19 |
|
|
Кальций |
Ca |
20 |
|
|
Скандий |
Sc |
21 |
|
|
Титан |
Ti |
22 |
|
|
Ванадий |
V |
23 |
|
|
Хром |
Cr |
24 |
|
|
Марганец |
Mn |
25 |
|
|
Железо |
Fe |
26 |
|
|
Кобальт |
Со |
27 |
|
|
Никель |
Ni |
28 |
|
|
Медь |
Cu |
29 |
|
|
Цинк |
Zn |
30 |
|
|
Галлий |
Ga |
31 |
|
|
Германий |
Ge |
32 |
|
|
Мышьяк |
As |
33 |
|
|
Селен |
Se |
34 |
|
|
Бром |
Br |
35 |
|
|
Криптон |
Kr |
36 |
|
При
возбуждении атомов в ходе их сближения изменяются волновые функции всех
валентных электронов, причем возникают новые волновые функции. Эти новые
волновые функции являются гибридными,
а само явление называется гибридизацией
волновых функций (или гибридизацией атомных орбит). Гибридизация атомных s- и p-орбиталей обеспечивает большее
перекрытие электронных орбит соединяющихся атомов, чем в случае негибридных
волновых функций. Благодаря этому не только упрочняются связи, но и понижается
энергия системы (кристалла). В зависимости от того, сколько p-орбиталей гибридизируется, различают sp1-, sp2- и
sp3-гибридные
орбиты. В случае sp1-гибридизации гибридные орбиты ориентированы по прямой линии в противоположные
стороны, т. е. составляют угол 180о. sp2-гибридизация
предполагает связи, находящиеся в одной плоскости под углом 120о
одна к другой. Для sp3-гибридизации характерно образование связей в тетраэдрическом виде
в четырех направлениях под углом ![]() .
.
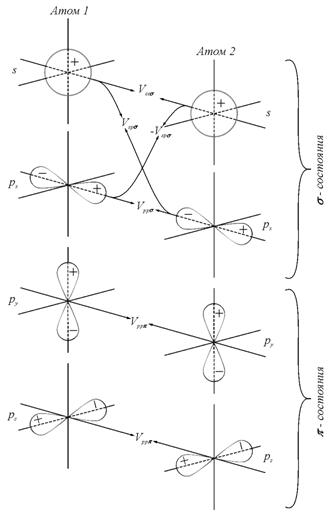
Связь при образовании молекулы может осуществляться перекрыванием различных типов орбиталей, ориентированных по-разному друг относительно друга. На рис. 2.17 показаны различные типы связи, возможные при образовании двухатомной молекулы лития. Перекрывание s- и p-орбиталей или p-орбиталей вдоль их осей ответственно за образование σ-связи, а перекрывание p-орбиталей в направлении, перпендикулярном их осям, ответственно за образование π-связи. Величина Vsps,p соответствует энергии взаимодействия при перекрытии различных типов орбиталей.
|
|
|
Рис. 2.17. Перекрытие атомных орбиталей в двухатомной молекуле лития и
результирующее состояние (справа) [31] |
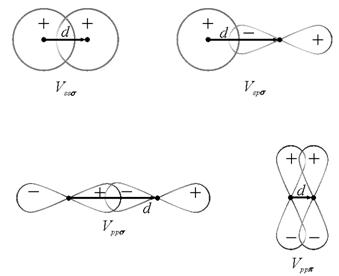
Четыре типа таких конфигураций проиллюстрировано на рис. 2.18,три из которых представляют s-связь и одна p-связь
|
|
|
Рис. 2.18. Четыре типа перекрытий волновых функций, иллюстрирующие s- и p-связи в двухатомной молекуле [31] |
Обычно значения энергии s-связи выше, чем значения энергии p-связи. Характерные значения энергии s- и p-связи для углерода, кремния, германия и арсенида галлия составляют Vsps=5,91; 2,54; 2,36; 2,36 эВ; Vppp=2,60; 1,12; 1,04; 1,04 эВ соответственно [31].