13.1. Термодинамические потенциалы
Любая термодинамическая система стремится к фазовому равновесию как к состоянию с наименьшей энергией. Необходимым условием равновесия является неизменность параметров системы (плотности, давления, температуры, и т. д.) с течением времени (стационарное состояние) и отсутствие в системе постоянных потоков (теплоты, вещества, и т. п.).
Термодинамическое равновесие системы характеризуется термодинамическими потенциалами. Все термодинамические параметры системы − давление p, объем V, температура T, и др. − могут быть получены как частные производные термодинамических потенциалов.
Основное уравнение термодинамики для равновесных процессов
|
TdS = dU + pdV, |
(13.1) |
где U – внутренняя энергия системы, S – ее энтропия.
Основное уравнение термодинамики связывает пять физических величин: температуру, давление, объем, энтропию и внутреннюю энергию (T, p, V, S, U). Для каждой пары из них существует термодинамический потенциал.
Если за
независимые переменные в уравнении (13.1) принять энтропию и объем (S и V), то для определения остальных
величин необходимо задать зависимость внутренней энергии от энтропии и объема.
Перепишем (13.1) как![]() , отсюда dU
является полным дифференциалом, и остальные параметры (температура и давление)
можно определить как:
, отсюда dU
является полным дифференциалом, и остальные параметры (температура и давление)
можно определить как:
|
|
(13.2) |
где индексы V и S означают, что система находится при постоянных объеме и энтропии соответственно.
Значит, для независимых переменных S и V внутренняя энергия U является термодинамическим потенциалом.
Рассмотрим другие варианты. Пусть независимыми переменными являются температура (T) и объем (V). Термодинамическим потенциалом в этом случае служит свободная энергия Гельмгольца F:
|
|
(13.3) |
Для независимых переменных T и p термодинамическим потенциалом является энергия Гиббса G:
|
|
(13.4) |
Энтальпия ![]() , также один из термодинамических потенциалов.
, также один из термодинамических потенциалов.
На практике наиболее удобными являются потенциалы Гиббса и Гельмгольца, поскольку переменные объем-температура (V, T) и давление-температура (p, T) могут быть экспериментально измерены.
Часто в
реальных термодинамических системах приходится иметь дело с переменным числом
частиц. Внутренняя энергия такой системы может меняться за счет изменения числа
частиц какого-либо сорта i на величину ![]() . Тогда основное уравнение термодинамики для таких систем
принимает вид
. Тогда основное уравнение термодинамики для таких систем
принимает вид
|
|
(13.5) |
Величина 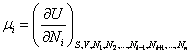 называется химическим потенциалом i-го сорта частиц и имеет смысл энергии, приходящейся на одну
частицу.
называется химическим потенциалом i-го сорта частиц и имеет смысл энергии, приходящейся на одну
частицу.
Для систем с
переменным числом частиц в выражения для дифференциалов свободной энергии и
потенциала Гиббса также будет входить дополнительный член ![]() . Следовательно, химический потенциал
. Следовательно, химический потенциал ![]() можно получить
дифференцированием любого из термодинамических потенциалов по числу частиц
можно получить
дифференцированием любого из термодинамических потенциалов по числу частиц
|
|
(13.6) |
Все термодинамические потенциалы являются экстенсивными величинами, т. е. они пропорциональны количеству вещества. Величины, не зависящие от количества вещества, называются интенсивными, к ним, например, относятся плотность, концентрация, температура. Экстенсивные величины выражаются математически однородными функциями, и для них справедлива теорема Эйлера об однородных функциях
|
|
где ![]() − экстенсивная величина.
Применяя эту теорему к термодинамическому потенциалу Гиббса, с учетом (13.6)
получим
− экстенсивная величина.
Применяя эту теорему к термодинамическому потенциалу Гиббса, с учетом (13.6)
получим
|
|
(13.7) |
Дальнейшие рассуждения будут базироваться на понятиях термодинамических потенциалов, введенных выше.
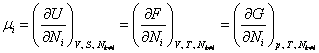 .
.