Операцию определения индексов называют индицированием. Индицирование проводят поразному для различных сингоний кристалла. Сингониями называют 7 кристаллографических систем. К одной сингонии относятся кристаллы, у которых одинаковы симметрия элементарной ячейки и кристаллографическая система осей координат. В табл. 5.2 приведены характеристики сингоний кристаллов.

Бравэ показал, что все многообразие кристаллических структур можно описать с помощью 14 типов решеток, отличающихся по форме элементарной ячейки и по симметрии. Решетки Бравэ определяют группу трансляций, характеризующую положение частиц в пространстве. Обозначения и координаты концов векторов трансляций относительно начала координат (базис ячейки) следующие: Р - примитивная, (000); I - объемноцентрированная, (000), (½½½); F - гранецентрированная, (000), (½½0), (½0½), (0½½); C - базоцентрированная, (000), (½½0).

Для примитивных решеток интенсивность отражений на рентгенограмме определяется формулой (5.2). Для остальных решеток Бравэ функция атомного рассеяния заменяется на амплитуду рассеяния сложной решеткой с базисом F_hkl , а атомный фактор рассеяния f² в формуле (5.2)соответственно на квадрат модуля структурной амплитуды |F_hkl|² . Структурная амплитуда:

     (5.6)

В формуле (5.6) M - число, а x_j, y_j, z_j - координаты атомов в элементарной ячейке. Экспоненциальный множитель учитывает сдвиг фаз волн, рассеянных различными атомами. Для однокомпонентных решеток формулу (5.6) можно записать как

     (5.7)

Таблица 2
Сингонии кристаллов и соответствующие им решетки Бравэ

* Гексагональную и тригональную сингонии описывают также в ромбоэдрической установке осей ( R ): a = b = c, α = β = γ ≠ 90° ; ось 3

Если решетка примитивная, то есть на ячейку приходится один атом с координатами (000), то фазовый множитель:
exp[i2π(hx_j + ky_j + lz_j)] = 1, F_hkl = f, |F_hkl|² = f², а I = f²L(Ψ₁Ψ₂Ψ₃).

Согласно (5.4) в этом случае индексы интерференции (h k l) - любые целые числа.

В случае объемноцентрированной элементарной ячейки с двумя одинаковыми атомами, находящимися в позициях (000) и (½½½), структурная амплитуда будет равна:
F_hkl = f{exp[i2π(h·0 + k·0 + l·0)] + exp[i2π(h·½ + k·½ + l·½)]} = f(1 + cos[π(h + k + l) / 2]} = f[1 +(-1)^(h+k+l)].

Сразу ясно, что если сумма индексов интерференции нечетная, то структурная амплитуда отражений с такими индексами будет равна нулю. Таким образом, на дифракционной картине кристалла с объемноцентрированной решеткой отсутствуют (гаснут) отражения, у которых сумма индексов интерференции нечетная. Это правило называется правилом погасания.

Нетрудно показать, что на дифракционной картине кристалла с гранецентрированной решеткой, на элементарную ячейку которого приходится четыре атома с координатами: (000), (½½0), (½0½), (0½½), гаснут отражения, у которых индексы интерференции имеют различную четность.

Большинство кристаллов имеет более сложную структуру, которую следует рассматривать как несколько вставленных друг в друга подрешеток. Так, решетка алмаза представляется в виде двух гранецентрированных кубических решеток, сдвинутых относительно друг друга на диагонали куба. В этом случае сохраняются все погасания гранецентрированных кристаллов, и появляются дополнительные погасания, обусловленные интерференцией волн, рассеянных каждой гранецентрированной подрешеткой.

В таблице 2 приведены индексы интерференции для простой кубической, ОЦК, ГЦК и алмазной решеток.

Таким образом, анализ структурных амплитуд опирается на явление интерференции и позволяет определить тип решетки Бравэ исследуемого однокомпонентного кристалла.

Если базис неизвестен, а в нашем распоряжении только экспериментально полученная дифракционная картина, то первым этапом определения структуры является индицирование, т. е. установление индексов (h k l) всех отражений, наблюдающихся на дифракционной картине данного кристалла.

Процесс индицирования основан на том, что значения межплоскостных расстояний d_hkl связаны со значениями периодов (a, b, c) и углов (α, β, γ) элементарной ячейки вполне определенными соотношениями. Простейшие из них приведены в таблице 3. С учетом уравнения Брэгга - Вульфа записывают также соотношения, которые называют квадратичными формами (табл. 3 ).

Таблица 3
Связь между величиной, обратной квадрату межплоскостных расстояний и периодами решетки и квадратичные формы

Задача индицирования дифракционных картин наиболее просто решается для кубических решеток. Из анализа квадратичной формы для кубических решеток следует, что отношение sin²θ_i каждого зарегистрированного i-го отражения к sin²θ₁ первого отражения равно отношению суммы квадратов индексов каждого i-го отражения к сумме квадратов индексов первого:

sin²θ_i/sin²θ₁ = . (5.8)

Следовательно, зная из эксперимента углы рассеяния sin²θ_i, можно рассчитать ряд чисел Q_Э = sin²θ_i/ sin²θ₁.

Сравнивая полученный ряд Q_Э с теоретически рассчитанным Q_T для различных типов кубических решеток (табл. 5.3), делают выводы о типе решетки и записывают индексы отражений.

Q_T = .

Для индицирования рентгенограмм кристаллов средних и низших сингоний также разработаны аналитические методы индицирования, и имеется целый ряд программ, позволяющих выполнить его для любых кристаллов. В частности, это программа IND пакета BASA и программа TREOR 90.

После проведения индицирования проводится определение периодов элементарной ячейки. Для кубических кристаллов период a = d_hkl . Однако, вследствие наличия систематических и случайных ошибок в дифракционном эксперименте, с одной стороны, и необходимости, как правило, получения прецизионных (высокой точности) данных с другой, нельзя окончательное значение периода найти путем простого усреднения значений, рассчитанных для отражений с различными индексами. Поэтому разработаны и используются специальные методики прецизионного определения периодов решетки [23].

Информация, получаемая из значений периодов элементарной ячейки и анализа их зависимостей от различных параметров, довольно обширна и разнообразна. Рассмотрим только некоторые примеры.

1. Если известна химическая формула и плотность исследуемого образца, то можно найти число формульных единиц (или атомов в случае простых веществ), приходящихся на элементарную ячейку. Поскольку оно должно быть целым, то это один из критериев корректности проведенного процесса индицирования и правильности определения размеров и формы элементарной ячейки. Обратная задача: зная размеры элементарной ячейки и число формульных единиц в ее объеме, можно найти плотность исследуемого вещества. Рассчитанное таким путем значение плотности называют рентгеновской плотностью материала.

2. Период элементарной ячейки зависит от состава вещества. В металлических двухкомпонентных твердых растворах с кубической структурой линейность зависимости периода решетки от концентрации компонентов (закон Вегарда) показывает, что это растворы с неограниченной растворимостью. Для высокотемпературных сверхпроводников (ВТСП) YBa₂Cu₃O_7-δ периоды элементарной ячейки зависят от индекса нестехиометричности δ (рис.21). В точке, где a = b происходит фазовый переход от ромбической сверхпроводящей фазы к тетрагональной несверхпроводящей.

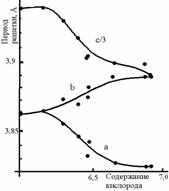
Рис. 21. Зависимость периодов a , b , c элементарной ячейки YBa₂Cu₃O_7-δ от индекса δ.

Таким образом, по зависимости периодов решетки от концентрации компонентов можно судить о наличии или отсутствии концентрационного фазового перехода в образцах.

3. Температурная зависимость периодов элементарной ячейки позволяет определить, с одной стороны, температуру термического фазового перехода, если он имеет место, с другой - величину коэффициента теплового расширения кристаллов α_Т, так как измеренное при температуре Т значение периода (a_Т) связано со значением, полученным при комнатной температуре, соотношением: a_Т = a₀ + α_ТТ. Это же соотношение справедливо и при замене периода решетки на межплоскостное расстояние d_hkl , и в этом случае мы можем проанализировать зависимость коэффициента теплового расширения кристаллов α_Т от кристаллографического направления hkl.

Индицирование дифракционной картины и определение периодов кристаллической решетки являются начальными этапами установления атомной структуры кристаллов, т.е. нахождения взаимного расположения атомов в элементарной ячейке.

Определение атомной структуры основано на анализе интенсивностей дифракционных максимумов. Интенсивность отражений I(2θ) пропорциональна квадрату модуля структурной амплитуды F_hkl, величина которой определяется значениями координат атомов в ячейке кристалла, см. формулу (5.6).

Для монокристаллических объектов дифракционная картина является трехмерной. Из полученных в эксперименте интенсивностей отражений после введения соответствующих поправок рассчитываются квадраты структурных амплитуд. Затем, используя один из методов решения системы нелинейных уравнений, находят значения координат атомов в элементарной ячейке. Следует отметить, что параллельно определяются величины тепловых смещений. Тепловое движение атомов в кристалле приводит к тому, что в формуле (5.6) функция атомного рассеяния f_j уменьшается с увеличением среднеквадратичных значений тепловых смещений атомов [u_j²] по экспоненциальному закону:

f_jT = f_jexp(-M_j).

Экспоненциальный множитель называется фактором Дебая - Валлера. В случае изотропных смещений M_j = 8π²[u_j²]sin²θ/λ². Величины среднеквадратичных тепловых смещений добавляются к значениям координат в качестве искомых параметров.

В поликристаллических объектах трехмерная дифракционная картина вырождается в одномерную, и задача определения атомной структуры резко усложняется. До недавнего времени по рентгенограммам поликристаллов проводили лишь уточнение значений координат атомов для кристаллов с известным характером взаимного расположения атомов. К настоящему времени порошковая дифрактометрия достигла настолько высокого уровня как в развитии технической базы, так и в разработке новых методик компьютерного анализа порошковых дифрактограмм, что исследователям удается надежно определить атомное строение материалов, содержащих до 30 и более атомов в независимой части элементарной ячейки.

Дифракционные методы позволяют также получать информацию о структурных характеристиках некристаллических материалов. В аморфных материалах нет трансляционной симметрии, т.е. нет дальнего порядка в расположении образующих его частиц. Однако в них сохраняется ближний порядок - упорядоченное расположение атомов (или молекул) в пределах нескольких межатомных расстояний.

Для изотропных некристаллических веществ регистрируемое в эксперименте распределение интенсивности рассеяния I(K), где K=4πsinθ/λ, представляет собой одномерную дифракционную картину. Из интерференционной части распределения интенсивности i(K)= I(K)- (суммирование проводится по числу атомов в формульной единице исследуемого соединения) рассчитывается радиальная функция распределения атомной или электронной плотности D(r):

D(r)=4πr²ρ(r)=4πr²ρ₀ + . (5.9)

Экпоненциальная функция вводится для уменьшения влияния ошибок эксперимента при больших значениях K, α обычно равно 0.1. На рис. 5.6 приведены соответствующие функции для аморфного окисла иттрия. Кривая радиального распределения электронной плотности D(r)=4πr²ρ(r) осциллирует около плавной кривой 4πr²ρ₀, определяемой величиной средней электронной плотности материала ρ₀. Положения максимумов на кривой D(r) соответствуют значениям наиболее вероятных межатомных расстояний - радиусам координационных сфер, площади под максимумами пропорциональны величинам координационных чисел - числам атомов на координационных сферах. Из ширины максимумов определяют размытия координационных сфер, характеризующие разброс межатомных расстояний относительно их средних значений. Подробно методика расчета рассмотрена в.

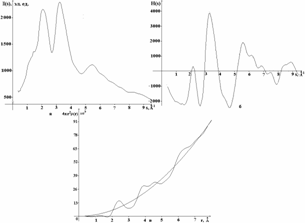
Рис.22. Кривые распределения: а) интенсивности рассеяния I(K) ; б) функции K_i(k)exp(-α²K²); в) радиальной функции распределения электронной плотности D(r) для аморфного окисла Y₂O₃

Таким образом, в целом все три дифракционных метода исследования (рентгено-, электроно- и нейтронография) являются прямыми методами изучения атомного строения материала и позволяют устанавливать взаимосвязь между структурным состоянием исследуемого материала и его физическими свойствами.

При обычно используемых в электронографии напряжениях от 20 до 100 кВ длины волн электронов находятся в пределах 0.08 - 0.03 Å. Малая длина волны позволяет получать четкую дифракционную картину от мелкодисперсных фаз. Малая проникающая способность и малая толщина вещества, необходимая для создания дифракционной картины, обеспечивает широкое применение электронографии при изучении тонких поверхностных слоев и специально приготовленных тонких пленок.

Длины волн тепловых нейтронов, используемых в нейтронографии, того же порядка, что и длины волн рентгеновского излучения. Однако разрешение нейтронограмм значительно хуже, чем разрешение рентгенограмм, и, как следствие, точность измерения межплоскостных расстояний составляет в лучшем случае 0.05 Å.

Преимущество нейтронографии, тем не менее, в том, что она позволяет устанавливать взаимное расположение атомов, являющихся соседями в таблице Менделеева, что весьма сложно сделать в случае проведения рентгенографического эксперимента. Широко используется нейтронография и для установления положений легких атомов в кристаллической решетке соединений. И наконец, поскольку нейтроны рассеиваются на магнитных моментах атомов, то нейтронография успешно применяется при изучении магнетиков - веществ, в направлениях магнитных моментов атомов которых имеется корреляция (вероятностная взаимосвязь). Так, именно с помощью магнитной нейтронографии установили существование антиферромагнитных и ферримагнитных структур [28].