Рентгеноструктурный анализ аморфных материалов
3. 5. Многократное рассеяние рентгеновских лучей аморфными материалами
Многократным рассеянием рентгеновских лучей называется одно из дифракционных явлений, при котором луч, отраженный от какого-либо семейства плоскостей в кристалле не выходит из образца, а вновь отражается (многократно) там же или иным семейством плоскостей. Направление распространения и интенсивность многократно отраженных лучей определяются условиями эксперимента и структурой исследуемого объекта [32]. Наряду с комптоновским и тепловым рассеянием, многократное рассеяние является одним из компонентов диффузного фона рентгенограмм.
При рассеянии кристаллическими материалами многократное рассеяние имеет сравнительно высокую интенсивность в малоугловой области : оно может полностью замаскировать рассеяние, возникающее на неоднородностях электронной плотности материала [32].
Основную часть многократного рассеяния составляет двойное (ДБР), и, как правило, достаточным является учет только его.
В поликристаллах возникает ДБР двух типов : внутризеренное - от плоскостей, принадлежащих одному зерну, и межзеренное - от плоскостей, принадлежащих различным, слегка разориентированным друг относительно друга зернам. ДБР в поликристаллах возникает под любым углом рассеяния, создавая на рентгенограмме диффузный фон, величина которого достигает нескольких электронных единиц на единицу состава.
Расчет интенсивности двойного рассеяния в поликристаллах производится по формуле:
(3.28)
где i, j - индексы, которыми обозначены два различных отражения : hi, ki, li и hj, kj, lj; pi, pj - факторы повторяемости для них; Fi2, Fj2 - структурные факторы : Р (2θ ) - фактор поляризации; A( θ,θ i ,θ j ) - функция, зависящая от углов ра c сеяния для i и j отражения и от угла θ , при котором производятся измерения.
Ко - некоторая постоянная для данного исследуемого вещества величина.
Полная интенсивность ДБР получается при суммировании по всем возможным для данного излучения комбинациям отражающих плоскостей.
Уоррен [33] считает, что схема возникновения двойного рассеяния в аморфных материалах аналогична той, что имеет место в поликристаллах. Малая величина областей ближнего упорядочения приводит к тому, что картина распределения интенсивности в аморфном материале непрерывна, то есть суммирование в (3.28) нужно заменить интегрированием.
Исходя из этого, Уоррен получил следующую формулу, позволяющую рассчитать поправку на двойное рассеяние:
(3.29)
Сумма по j - сумма по формульной единице произведений атомного веса ( A.в.) на массовый коэффициент поглощения j-го компонента; NA - число Авогадро; I(2θ) - интен-сивность рассеяния, измеряемая в точке наблюдения; РD(θ) - поляризационный фактор.
Если неполяризованное излучение рассеивается вначале под углом 2θ 1 , а затем рассеянный пучок еще раз отражается под углом 2θ 2 таким образом, что его направление образует с первичным лучом угол 2θ (рис. 19), то поляризационный фактор будет иметь вид :
(3.30)
Рис.19. Схема возникновения двойного рассеяния при съемке на отражение [33]
Обозначим: q1=cos(2θ1), q2=cos(2θ2); ε - угол, который определяет направление луча, рассеянного под углом 2θ1, образует с горизонтальной плоскостью XY (рис.19). Из сфе-рических треугольников (рис. 20) следует:
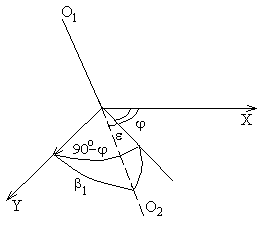
Риc. 20 . Сферический треугольник, используемый для расчета q1 и q2 через углы θ, φ и ε [34], O1 - точка, в которой первый раз рассеивается падающий луч; O2 - точка, в которой происхо-дит повторное рассеяние.
где φ - угол, образованный проекцией направления луча, рассеянного под углом 2 ν 1 на плоскость ХY, и осью X (рис. 19, 20);
I (q 1 ) - интенсивность, рассеянная под углом 2 θ 1 в электронных единицах на единицу состава;
I (q 2 ) - интенсивность, рассеянная вторично под углом 2 θ 2 в электронных единицах на единицу состава.
Поскольку интегрирование в (3.29) приводит просто к усреднению по всей области углов рассеяния, для аморфных материалов с хорошей степенью точности можно заменить
I (q) на интенсивность независимого рассеяния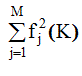 
. При этом в зависимости от условий эксперимента можно брать либо
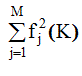, либо 
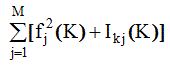- сумму комптоновского и независимого рассеяния.
Характер зависимости I (q) от угла рассеяния 2θ таков, что приблизительно ее можно представить как
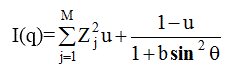(3.31)
Коэффициенты u и b ищутся путем подбора, причем если задается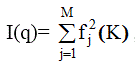 
, то, как правило, q = 0. Записав отношение I2/I1 в виде;
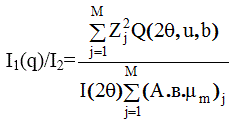(3.32)
Уоррен рассчитал и протабулировал функцию Q(2θ,u,b) для ряда значений 2θ, u и b (таблица 6).
Таблица б
Значения функции Q(2θ,u,b)·!0 4 , по данным работы [32]
u= 0,00
|
Ν |
b=10 |
b=20 |
b=40 |
b=60 |
b=80 |
b=100 |
|
30 |
192 |
104 |
50,8 |
31,3 |
21,6 |
16,0 |
|
60 |
196 |
87 |
33,7 |
18,3 |
11,7 |
8,1 |
|
90 |
164 |
64 |
22,2 |
11,5 |
7,1 |
4,8 |
|
120 |
124 |
45 |
14.9 |
7,6 |
4,6 |
3,2 |
|
150 |
103 |
36 |
11,9 |
6,0 |
3,7 |
2,5 |
|
180 |
98 |
34 |
11,1 |
5,6 |
3,4 |
2,3 |
u = 0,05
|
Ν |
b=10 |
b=20 |
b=40 |
b=60 |
в=80 |
b=100 |
|
30 |
219 |
126 |
68,1 |
46,2 |
34,9 |
28,1 |
|
60 |
238 |
121 |
59,1 |
39,4 |
30,1 |
24,7 |
|
90 |
218 |
105 |
51,9 |
35,7 |
28,1 |
23,7 |
|
120 |
179 |
86 |
43,9 |
31,1 |
25 |
21,4 |
|
150 |
156 |
75 |
39,4 |
28,3 |
23 |
19,8 |
|
180 |
130 |
73 |
38,1 |
27,5 |
22,4 |
19,4 |
u= 0,10
|
Ν |
b=10 |
b=20 |
b=40 |
b=60 |
b=80 |
b=100 |
|
30 |
250 |
154 |
92 |
68 |
55 |
47 |
|
60 |
287 |
163 |
93 |
70 |
58 |
51 |
|
90 |
279 |
155 |
92 |
71 |
61 |
54 |
|
120 |
241 |
136 |
83 |
66 |
57 |
51 |
|
150 |
216 |
123 |
77 |
61 |
53 |
48 |
|
180 |
209 |
120 |
75 |
60 |
52 |
47 |
u= 0,20
|
Ν |
b=10 |
b=20 |
b=40 |
b=60 |
b=80 |
b=100 |
|
30 |
326 |
225 |
157 |
130 |
115 |
106 |
|
60 |
402 |
268 |
188 |
159 |
144 |
134 |
|
90 |
423 |
283 |
204 |
175 |
160 |
157 |
|
120 |
386 |
263 |
193 |
168 |
154 |
146 |
|
150 |
355 |
244 |
182 |
158 |
146 |
138 |
|
180 |
347 |
239 |
178 |
156 |
143 |
136 |
Для материалов с низким коэффициентов поглощения двойное рассеяние оказывается настолько велико, что пренебрегать им при расчетах нельзя : так, для SiO2 на Rh К α излучении I2/I1 ≈0,08 в области углов 2θ от 900 до 180 0.
Анализ влияния двойного рассеяния на интенсивность дифракции аморфными материалами при дифрактометрии на прохождение проведен в работе [34]. Схема возникновения двойного рассеяния в образцах, имеющих конечную толщину и исследуемых на прохождение, показана на рис. 21.
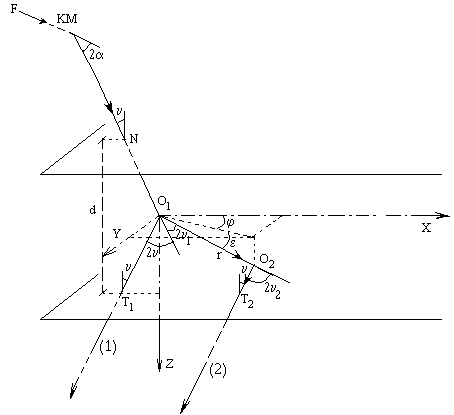
Рис.21. Ход лучей при возникновении двойного рассеяния в случае дифрактометрии на прохождение;
F - фокус трубки; KM - кристалл-монохроматор, угол рассеяния которого 2 α. Лучи О 1 Т 1 и О 2 Т 2 параллельны друг другу, d - толщина образца [34]
Падающее на образец излучение частично поляризовано кристаллом-монохроматором. Отношение I2/I1 в этом случае описывается в виде:
(3.33)
Здесь N - число формульных единиц в единице объема; P(2θ)- поляризационный фак-тор (3.5); A(2θ) - фактор поглощения для случая съемки на прохождение, формула (3.8); A2(2θ) - фактор поглощения для двойного рассеяния:
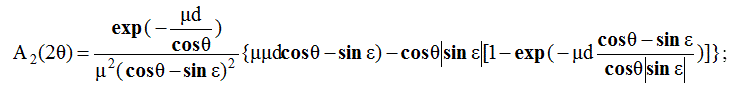(3.34)
P2 - поляризационный фактор для двойного рассеяния,
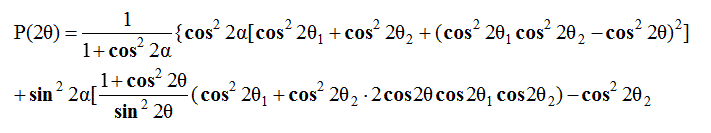
(3.35)
Причем исходя из сферической тригонометрии
cos(2θ1)=cosθ sinε + cosε sinθcosφ
cos(2θ2)=cosθ sinε - cosε sinθcosφ
Относительная интенсивность ДБР для азоксифенетола на МоК α излучении при d = 0,4 см приведена на рис. 22
Рис.22. Распределение интенсивности рассеяния I(2 ν) и отношение I2/I1 для азоксифенетола на МоК α излучении [34].
Начиная с 2θMo = 80° (К = 11,5 Ao -1 ), величина поправки на двойное рассеяние для тонких образцов при исследованиях на прохождение превышает 10 %, а при К~К max , достигает 30 %.
Таким образом, при исследовании материалов с малыми значениями коэффициента поглощения нельзя пренебрегать поправкой на многократное рассеяние.