Рентгеноструктурный анализ аморфных материалов
2.4. Скопление многоатомных молекул с жесткими и внутримолекулярными связями.
Рассмотрим рассеяние рентгеновского излучения конфигурацией из N молекул, заключенных в объеме V. Все молекулы одинаковы, каждая состоит из n атомов в общем случае разного сорта. Связи внутри молекул жесткие. Последнее означает, что как в данной молекуле с течением времени, так и при переходе от одной молекулы к другой величины длин и углов связей между атомами внутри молекулы не изменяются.
В уравнении (2.1) теперь суммирование должно производится как по числу молекул N , так и по числу атомов в молекуле n.
Соответствующее выражение для интенсивности рассеяния можно представить в виде:
(2.27)
здесь μ,ν - номера молекул ;
- радиус- векторы, соединяющие центр скопления
молекул О с атомом р в молекуле m и атомом q в молекуле n соответственно (рис.6).
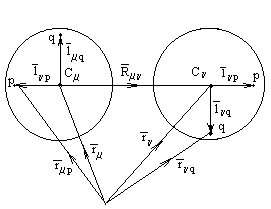
Рис.6. Схема, поясняющая обозначения расстояния между атомами в материале, состоящем из сложных молекул[ I]
Обозначим через 
и 
- расстояния
от центра скопления до центров молекул m и n :
и 
-
расстояния от центра данной молекулы до соответствующих атомов внутри нее.
Тогда (2.27) перепишется в виде:
. (2.28)
В формуле (2.28) можно выделять два типа слагаемых:
а) При μ=ν получаем:
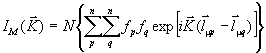(2.29)
Кривая 
отвечает вкладу в суммарное рассеяние внутримолекулярных интерференционных
эффектов, то есть эффектов, обусловленных порядком в расположении атомов внутри молекулы.
б) при 
(2.30)
Проанализируем ситуации, когда 
пренебрежимо мало, то есть рассмотрим случай полного
отсутствия корреляции в расположении молекул. Вся рассеянная интенсивность будет определяться выражением (2.29), но вследствие
хаотичности распределения молекул по ориентациям Относительно дифракционного вектора необходимо экспоненту в (2.29) усреднить.
Выделяя слагаемые с p=q , и обозначая 
, получим :
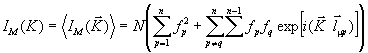(2.31)
Усреднение проводится по ориентациям вектора 
относительно 
.
Скалярное произведение 
, а вероятность того, что вектор 
составляет
с 
угол, заключенный в интервале a, a+ d a равна 
Следовательно,
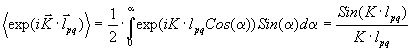(2.32)
Из (2.31) и (2.32) имеем
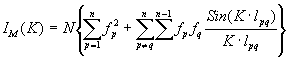(2.33)
IM (К) - средняя интенсивность рассеяния скоплением из хаотически ориентированных одинаковых молекул с жесткой внутримолекулярной
конфигурацией атомов. Выражение (2 . 33) неприменимо при К =0, так как оно дает значение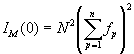 
,
тогда как в действительности, исходя из проведенного в разделе 2.2 анализа, IM(0) должно равняться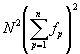 
.
Причина такого несоответствия заключается в том, что при выводе (2.33) из (2.30) мы пренебрегаем слагаемыми, в которых атом р находится в одной молекуле, а атом q - в другой :
где атомы р и q принадлежат разным молекулам. Когда 
= 0 эта сумма равна 
полное значение 
.
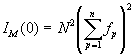Фактически это учет рассеяния неупорядоченной конфигурацией точечных одинаковых молекул, заключенных в сферическом объеме V.
Из уравнения (2.33) следует, что для каждой пары атомов в молекуле существует интерференционный член, а на долю, вносимую этой парой в рассеяние, оказывает влияние не направление линии, соединяющей атомы, а только ее длина.
В частности, для двухатомной молекулы (2.33) перепишется в виде :
(2.34)
Если f1=f2=f , а l12=l, то
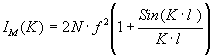(2.35)
Второе слагаемое в (2.35) - интерференционный член, обусловленный расположением атомов в каждой молекуле в группы по
два на определенном расстоянии l друг от друга. Без учета малоуглового рассеяния величина 
при 
приближается к 4f2, при 
.
В промежуточной области кривая имеет ряд минимумов и максимумов, которые соответствуют диффузным
гало вокруг первичного пучка. Появление этих пиков обусловлено поведением второго слагаемого в формуле (2.35) и связано с внутримолекулярными
интерференционными эффектами. В таблице. 1 приведены значения К l и Sin(θ) , при которых функция — имеет максимальные значения.
Таблица I
Значения К l и Sin(θ), при которых 
имеет максимум
|
№. max |
1 |
2 |
3 |
… |
m |
|
Kl |
2,46 p |
4,477 p |
6,484 p |
… |
(2m+0.5) p |
|
Sin( u ) |
|
|
|
… |
|
Эренфест вывел формулу, связывающую положение первого максимума u max на кривой IM (К) с величиной кратчайшего межатомного расстояния l1 , по аналогии с уравнением Вульфа -Брэгга в виде 2l1Sin u 1max=1.23 l Таким образом, зная положение первого максимума на кривой I(K ) для систем, состоящих из атомов одного сорта, можно оценить l1.
Если молекула состоит из нескольких атомов, то число интерференционных членов будет определяться числом межатомных расстояний, встречавшихся в данной молекуле. Если число межатомных расстояний велико и все они различны, то есть молекула имеет неправильную форму, то результирующая интерференционная картина будет размыта. По мере приближения формы молекулы к правильной и возрастания числа одинаковых межатомных расстояний контрастность дифракционной картины возрастает: появляются отчетливые максимумы и минимумы .
Если кратчайшие расстояния между молекулами в исследуемом веществе приближаются по величине к диаметру молекулы, то на внутренние интерференционные эффекты, обусловленные порядком в расположении атомов внутри молекулы, накладываются внешние интерференционные эффекты, связанные с межмолекулярным ближним порядком.
Распределение интенсивности рассеяния, соответствующее межмолекулярным эффектам, описывается формулой (2.30), причем вектор 
представляет собой расстояние между центрами молекул m и n (рис.6).
Исходя из выражения (1.4) вероятность d р( R ) нахождения центра молекулы n в сферическом слое толщиной dR , находящемся на расстоянии 
от центра молекулы m будет для изотропной системы молекул
(2.36)
Считая, что W(R ) одинакова для любой пары разных молекул, и проводя усреднение по конфигурациям аналогично тому, как это было сделано при выводе формулы (2.16), получим для средней интенсивности рассеяния выражение :
(2.37)
Положение атома р в молекуле m , описываемое вектором 
, совершенно не зависит от того, где при этом находится атом q в молекуле n . Это означает, что в формуле (2.37) 
можно представить в виде произведения двух сомножителей, каждый из которых усредняется по ориентациям соответствуящей молекулы в пространстве полностью независимо от другого. Обозначив 
, получим для среднего значения экспоненты
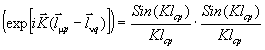(2.38)
Обозначив
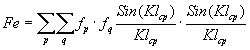(2.39)
запишем для I мм (К):
(2.40)
Суммарная интенсивность рассеяния, обусловленная как внутри, так и межмолекулярной корреляцией, имеет вид :
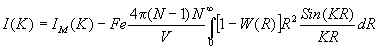(2.41)
Формула (2.41) впервые была получена Менка.
Здесь функция W(R) - радиальная функция распределения молекул, позволяющая определить наиболее вероятные межмолекулярные расстояния.
Функцию радиального распределения молекулярной плотности rM (R) можно найти Фурье - преобразованием функции j (K), (2.42)
(2.42)
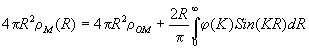(2.43)
средняя молекулярная плотность.
Для нахождения функции j (К) необходимо иметь экспериментальные значения интенсивности рассеяния I(K) исследуемым скоплением молекул. 1м(К) можно рассчитать, зная расположение атомов внутри молекулы. Кроме того, экспериментально можно измерить 1м(К), если есть возможность провести исследования разреженного газа, состоящего из данных молекул.
Функция F е рассчитывается также исходя из внутримолекулярной конфигурации атомов. Нужно отметить при этом, что вид функции Fе будет зависеть от выбора центра молекулы (С). Поскольку интенсивность рассеяния не может зависеть от такого выбора, то очевидно , что от положения С в молекуле будет зависеть вид функции W(R).