Элементы рентгеноструктурного анализа - глава для повторения
ЭЛЕМЕНТЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА
1. ПРИРОДА РЕНТГЕНОВСКИХ ЛУЧЕЙ
Рентгеновские лучи - это электромагнитные волны, обладающие сравнительно короткой длиной от 10-4 до 102 А. Коэффициент преломления рентгеновских лучей мало отличается от единицы: n=1—δ, где δ=10-6—10-5.
Так же, как и световые лучи, рентгеновские лучи могут быть линейно-поляризованными.
Сплошной спектр рентгеновских лучей возникает при резком торможении падающих на анод электронов. Из электродинамики известно, что в процессе торможения электрического заряда в поле ядер атомов анода возникает электромагнитный импульс, который можно рассматривать как сумму бесконечно большого числа колебаний различных длин волн, изменяющихся от min до бесконечности (рис. 1).
Существование коротковолновой границы сплошного спектра хорошо объясняется квантовой теорией. При торможении электрона его кинетическая энергия E=eU, где е — заряд электрона, U — напряжение, может полностью перейти в энергию одного фотона. При этом
hνmax= eU или h(c/λmin)=eU;
откуда
λmin=hc/ eU=12,39/U Ǻ
если U в кВ.
Характеристический спектр рентгеновских лучей возникает при повышении ускоряющего напряжения на трубке. При некотором, определенном для каждого материала напряжении на фоне непрерывного спектра появляются максимумы линейного спектра, который является характеристикой материала анода (рис. 61). Характеристический спектр содержит линии нескольких серий. Для тяжелых элементов установлено наличие К-, L-, М-, N-, 0-серий. Излучение каждой серии появляется только при достижении определенного значения напряжения, называемого потенциалом возбуждения.
Рисунок 1:
Распределение интенсивности в сплошном спектре рентгеновского излучения и распределение интенсивности в спектре излучения молибденовой трубки.
Например, потенциал возбуждения К-серии железа равен 7,10; меди— 8,86; молибдена — 20,0 кВ.
Спектры характеристического излучения различных элементов одинаковы по своему строению, а их особенности обусловлены строением электронных оболочек атомов. При увеличении атомного номера элемента анода наблюдается смещение характеристического спектра в сторону коротких волн, т. е. высоких частот. Эта закономерность установлена Мозли, она записывается в виде
(ν)-2=p(z-σ),
где р - константа, соответствующая данной линии; z—порядковый номер элемента; б—поправка на экранирование заряда ядра электронами.
Появление линий характеристического спектра обусловлено переходами электронов на внутренние оболочки атомов. Так, переход электронов с L- на K-оболочку приводит к появлению Кα1 и Ka2 - линий, с М- на К — Kβ линий. При рассмотрении возникновения серий характеристического излучения необходимо учитывать строение энергетических уровней атома.
2. ВЗАИМОДЕЙСТВИЕ РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
При прохождении рентгеновских лучей через вещество всегда наблюдается ослабление излучения за счет поглощения и рассеяния. В общем случае интенсивность лучей, прошедших через слой вещества толщиной d, подчиняется зависимости
I=I0ехр (—мd),
где I0 — интенсивность падающего пучка рентгеновских лучей; м—линейный коэффициент ослабления.
Обычно пользуются так называемым массовым коэффициентом ослабления мm=м/p где р—плотность вещества. Коэффициент ослабления можно представить в виде
μ/ρ=τ/ρ+ τ/ρ +π/ρ
где τ/ρ — коэффициент фотоэлектрического поглощения, зависящий от энергии падающего излучения; τ/ρ — коэффициент рассеяния; π/ρ — коэффициент, характеризующий образование электронно-позитронных пар (при энергии излучения большей, чем 1,022 МэВ). В реальном случае (т. е. при энергии излучения меньшей, чем 0,5 МэВ) основной вклад в ослабление вносит фотоэлектрическое поглощение. Зависимость коэффициента фотоэлектрического поглощения от длины волны используется в селективных фильтрах.
3. ЭЛЕМЕНТЫ КИНЕМАТИЧЕСКОЙ ТЕОРИИ РАССЕЯНИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
В кинематической теории рассеяния рентгеновских
лучей взаимодействием между первичным и рассеянным излучением пренебрегают,
т. е. не учитывается многоволновое рассеяние. Кристалл предполагается
несовершенным, состоящим из слегка разориентированных блоков (блоков мозаики),
имеющих совершенную структуру. Для подсчета интенсивности рассеяния от всего
кристалла суммируются интенсивности рассеяния отдельными блоками.
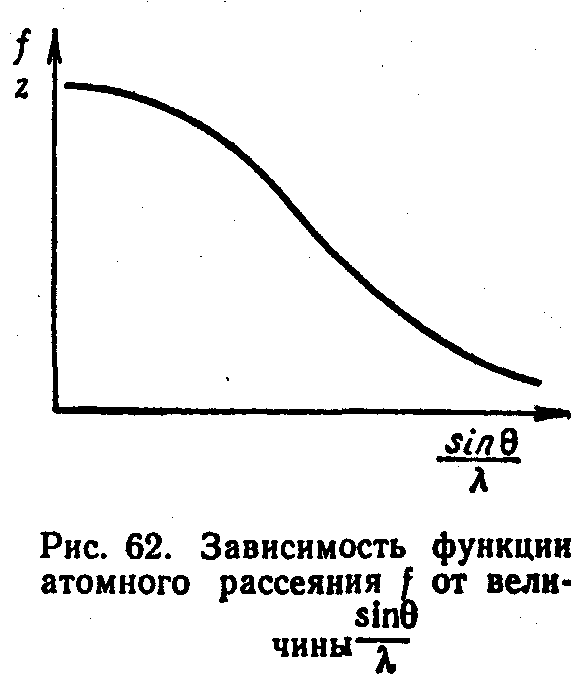
Атомный множитель. Излучение, рассеянное отдельными электронами атома, не совпадает по фазе вследствие того, что электроны не локализованы в одной точке пространства. Поэтому амплитуда волны, рассеянной атомом, всегда меньше суммы амплитуд волн, рассеянных всеми электронами атома. Для учета этого явления вводится так называемая функция (множитель) атомного рассеяния f, которая численно равна отношению амплитуды волны, рассеянной атомом, к амплитуде волны, рассеянной одним электроном. Квадрат функции атомного рассеяния является отношением интенсивности излучения, рассеянного атомом, к интенсивности излучения, рассеянного одним электроном.
Полагая, что распределение электронов ρ(r) в атоме обладает сферической симметрией, функция атомного рассеяния определяется как
f=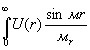
dr
где м=4π(sin θ/λ); U(r)=4πr2ρ(r)
Функция атомного рассеяния зависит от величины θ и отношения sin θ/λ (рис.2). В предельном случае (sin θ/λ =0) она числено равна величине полного заряда атома z, что свидетельствует о совпадении направлений рассеянной и падающей волн. При определении величины f иногда следует учитывать эффект дисперсии и вводить соответствующие поправки.
Структурный множитель. При исследовании кристаллов со сложными решетками наблюдается изменение дифракционной картины за счет изменения фазовых соотношении взаимодействия волн, рассеянных от различных плоскостей. Амплитуда волны, рассеянной сложной решеткой, равна сумме амплитуд (с учетом разностей их фаз) волн, рассеянных простыми подрешетками. Выражение для структурной амплитуды можно записать в виде
F(HKL)=∑ fj exp[-2πi(Hxj+Kyj+Lzj)]
где fj — функция атомного рассеяния; H=nh, K=nk, L=nl; Xjj Yj Zj — координаты атомов базиса. Для расчетов часто пользуются тригонометрической формой записи:
F(HKL)=∑fj[cos2πi(Hxj+Kyj+Lzj)-isin2π (Hxj+Kyj+Lzj)
Интенсивность пропорциональна квадрату структурной амплитуды. Следовательно, структурный множитель интенсивности равен
│F(HKL)│2=[∑fj[cos2πi(Hxj+Kyj+Lzj)]2-[sin2π (Hxj+Kyj+Lzj)]2
При наличии в структуре центра симметрии член с синусом обращается в нуль.
Таким образом, структурный множитель интенсивности для любой пространственной решетки определяется только координатами и функцией атомного рассеяния базиса.
Температурный множитель (фактор Дебая—Валлера). Атомы находятся в состоянии непрерывных тепловых колебаний относительно узлов кристаллической решетки. Такие смещения могут достигать значительной величины даже при комнатной температуре. Это явление приводит к изменению разности фаз рассеянного излучения, что сказывается на интенсивности рефлексов рентгенограммы. Следует заметить, что тепловые колебания не только уменьшают интенсивность рефлексов последней, но также увеличивают интенсивность диффузного фона.
Теоретический расчет теплового множителя интенсивности для реальных кристаллов представляет собой довольно сложную задачу, для решения которой необходимо знание всего спектра колебаний решетки. Интенсивность дифракционных рефлексов под действием температуры изменяется согласно выражению
IТ=I0ехр (—2М),
где I0 — интенсивность отражения при 0 К;
М = 8π<Ū2> sin2 θ/λ2
Более строгий вывод приводит к следующему выражению:
М =(6h2/mkθ)[Ф(х)/x+1/4] sin2 θ/λ2
где h — постоянная Планка; k — постоянная Больцмана;
m — масса атома; Ф(х)/x — функция Дебая; θ — характеристическая температура. Слагаемое 1/4 учитывает колебания при абсолютном нуле.
Если решетка содержит несколько сортов атомов, то, очевидно, тепловые множители этих атомов будут различаться. Кроме того, при высоких температурах становятся существенными поправки, обусловленные ангармонизмом колебаний.
Угловой множитель. Угловой множитель интенсивности, вообще говоря, включает в себя поляризационный и лоренцевский множители и учитывает зависимость интенсивности рассеяния рентгеновского излучения электроном от угла. При съемке поликристаллического образца на дифрактометре угловой множитель имеет вид
PLG=[1+cos22θ]/sin2θcosθ
Абсорбционный множитель. Абсорбционный множитель А(θ) учитывает поглощение рентгеновских лучей в образце и в общем случае зависит от его формы, коэффициента поглощения лучей образцом м, угла отражения θ. При съемке на дифрактометре (на отражение) абсорбционный множитель не зависит от угла θ и равен м/2.
Множитель повторяемости. Множитель повторяемости Р учитывает число эквивалентных плоскостей, участвующих в данном отражении. Он зависит от индексов плоскости и не зависит от угла отражения, в значительной степени зависит от симметрии решетки исследуемого кристалла. С понижением симметрии решетки величина множителя повторяемости уменьшается.
Таким образом, с учетом всех перечисленных множителей интенсивности общее выражение для интенсивности отражения от поликристаллического образца запишется так:
I=I0*K*PLG*│F│2*e –2M* А(θ)*P
где I0—интенсивность первичного пучка; К—постоянный множитель, объединяющий общие для всех рефлексов константы.