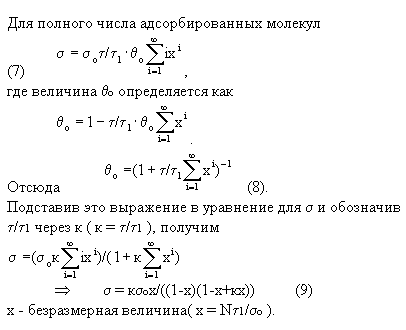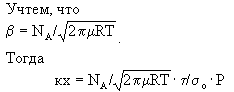Изотермы адсорбции

     Важнейшим понятием при описании явления адсорбции является среднее время жизни молекул на поверхности, или время адсорбции. Это время, в течении которого атом находится на поверхности адсорбата.
      Рассмотрим молекулу газа, приближающуюся к поверхности твердого тела. В отсутствие сил притяжения между молекулой и твердым телом, время, в течении которого молекула находится вблизи поверхности, должно быть ~ 10^-13
с(период молекулярных колебаний), а коэффициент аккомодации(прилипания) =0. Тогда происходит зеркальное отражение молекулы.
    Если между молекулой и поверхностью действуют силы притяжения, то, согласно уравнению Френкеля, среднее время жизни молекулы на поверхности
t = t_oexp(Q/RT) (1),
где t₀ - время молекулярных колебаний, Q - энергия взаимодействия молекулы с поверхностью(теплота адсорбции). Разумно считать, что адсорбция имеет место, если  достигает хотя бы нескольких периодов молекулярных колебаний.
     Кроме Q и t, важное значение имеет концентрация молекул на поверхности s. Согласно основному уравнению адсорбции,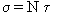 (2),
где N - число ударов молекулы о единицу поверхности за единицу времени.
Простейшая форма изотермы адсорбции.
 Подставляем в (2) N из ( N=1/4 n vt ) и t из (1), получаем
 .
    При адсорбции данного газа на поверхности данного адсорбента величины m и t_o постоянны, поэтому можно написать

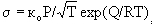
где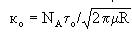
    Eсли зафиксировать Т=const, то s = k₁ Р, т.е. количество адсорбированного газа прямо пропорционально давлению. Это уравнение является уравнением изотермы адсорбции. Это простейшее уравнение для изотермы адсорбции и оно справедливо только тогда, когда отсутствует какое-либо взаимное влияние адсорбированных молекул. Дополнительно предполагается, что Q одинакова для всех молекул. На практике эти условия выполняются, когда число адсорбированных молекул мало.

Изотерма адсорбции Лэнгмюра.
 Если степень покрытия не мала, то имеет место взаимное влияние адсорбированных молекул. Это влияние может проявляться в том, что адсорбированные молекулы мешают поступлению других из газовой фазы.
Рассмотрим поверхность, на которой уже адсорбировано некоторое количество молекул. В этом случае ударяющаяся молекула может попасть не на свободный участок, а столкнуться с адсорбированной молекулой.
 Лэнгмюр предположил(1916г.), что молекулы, ударяющиеся об адсорбированные молекулы, либо отрожаются, либо связываются на столь короткое время, что практически не участвуют в адсорбции.

Отсюда следует, что адсорбированный слой должен быть мономолекулярным.
 Лэнгмюр сделал два допущения:
1) Теплота адсорбции(Qадс.) всех молекул, ударяющихся о свободную поверхность, одна и та же и не зависит от присутствия других адсорбированных молекул.
2) Каждая молекула, ударяющаяся об адсорбированную молекулу, немедленно возвращается в газовую фазу (что приводит к концепции мономолекулярного слоя).
      Максимальная адсорбция будет иметь место при полном покрытии поверхности слоем адсорбированных молекул с двумерной плотной упаковкой, и на поверхности этого монослоя не будет происходить никакой адсорбции.
      В основе вывода изотермы адсорбции Лэнгмюра лежит разделение скоростей испарения и конденсации молекул при динамическом равновесии между адсорбированной фазой и газом. Предполагается, что на поверхности имеется определенное число мест(центров) адсорбции, занимающих площадь S. Часть этой площади S₁ - занята адсорбированными молекулами, а другая часть s₀=S-S₁ - свободна. Скорость испарения пропорциональна S₁ cvисп ~k₁S₁. Скорость испарения пропорциональна(~) s₀ и давлению газа, т.е. равна к2Рs₀.
     В равновесии k₁S₁=к2Рs₀=к2Р(S-S₁).
Учтем, что S₁/S= J - степень покрытия(доля поверхности, занятая адсорбированными молекулами). Тогда J = bP/(1+bP), где b=к2/k₁ - постоянная Лэнгмюра.
     Примеры изотермы адсорбции Лэнгмюра для различных t(t1>t2>t3).
{ГРАФИК}
     Можно заменить J на v/vm, где vm - объем адсорбированного газа при монослойном заполнении, v - объем фактически адсорбированного газа, тогда v=vmbP/(1+bP)
 При низком давлении u ~ Р, при Р®Ґ v®Ґ.
Уравнение можно привести к линейному виду Р/v=1/bvm
+P/vm.
Здесь зависимость Р/v от Р есть прямая. По углу и отрезку, отсекаемому по оси ординат, можно найти vm и b.

Если x - удельная поверхность твердого тела, то vm=xvо/NASмол.,
где Sмол. - площадь, приходящаяся на одну адсорбированную молекулу в монослое или величина посадочной площади; uо - объем одного моля газа при нормальных условиях(22,4л); NA - число Авогадро.
Таким образом при известном Sмол. по величине um можно рассчитать x - удельную поверхность. Если адсорбировать несколько газов к-компонент, то для i-ой компоненты


Изотерма полимолекулярной адсорбции.
 Если молекулы, ударяющиеся об адсорбированный слой, испытывают достаточное притяжение, то временем пребывания их на поверхности пренебречь нельзя. В этом случае выполняются условия для полимолекулярной адсорбции.
 Лэнгмюр, а так же другие авторы пытались вывести уравнение полимолекулярной адсорбции. Однако наиболее удачная попытка сделана Брунауэром, Эмметом и Толлером в 1939г.
 Они сделали допущение, что в процессе образования слоя адсорбированные молекулы этого слоя не оказывают взаимного влияния друг на друга. Они также предположили, что энергия адсобции первого слоя постоянна и постоянна энергия адсорбции в пределах каждого из последующих слоев.

Обозначим через J1 долю поерхностии, покрытую слоем в одну молекулу, J2 - в две и т.д.. Полное число молекул,адсорбированных на единицу площади равно
s = s₀J1+2s₀J2+3s₀J3+...is₀Ji+...
где s₀ - число молекул на единицу площади в заполненном монослое.
Таким образом,
 
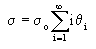
при равновесии все значения Ji постоянны. Это значит, что непокрытая часть поверхности тоже постоянна. Обозначим ее через Jо :

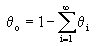
Число молекул, ударяющихся о Jо и адсорбирующихся там (NJо), должно быть равно ns₀J1 - числу молекул, испаряющихся с поверхности J1.
 NJо=ns₀J1 (1)
N - число молекул, ударяющихся о единицу поверхности в единицу времени,

n - коэффициент пропорциональности, имеющий размерность [1/c].
Аналогично, доля J1 определяется молекулами, адсорбированными на непокрытой части поверхности (NJо) и молекулами, испаряющимися с поверхности второго слоя (n1s₀J2) с одной стороны и молекулами, испаряющимися с J1 (ns₀J1) и адсорбированными на J1 (NJ1) с другой стороны
 NJо+n1s₀J2=ns₀J1+NJ1 (2)

из (1) ® (2) [NJо] Ю ns₀J1+n1s₀J2=ns₀J1+NJ1 Ю
 n1s₀J2=NJ1 (3)
Аналогично для i-ой поверхности NJi-1=ni-1s₀Ji (4)
вместо ni введем ti=1/ni - время адсорбции.
Получим систему уравнений
мs₀J1=NJ_ot
нs₀J2=NJ₁t1_________(5)
п    ...........
оs₀Ji=NJi-1ti-1
Допустим, что t₁=t₂=...=t_i (Это значит, что время адсорбции молекулы, расположенной поверх другой адсорбированной молекулы того же типа, не зависит от числа слоев.)

Такое допущение весьма правдоподобно, поскольку силы взаимного притяжения примерно одинаковы.
Тогда систему можно упростить:
мJ2=xJ1
нJ3=xJ2=x2J1 ______(6)
п   ...........
оJi=xi-1J1 ,
где x=Nt₁/s₀ Ю Ji=t/t₁ЧJоxi ( Jо - непокрытая часть поверхности.)
Кроме того J1=Nt/s₀ЧJо = хt/t₁ЧJо.

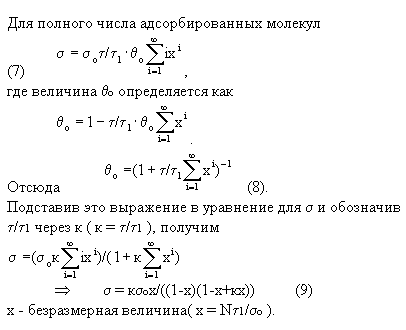
Учтем, что

 Ю  х = bt1/s₀ЧP (10)
 Величина s₀/bt1 имеет размерность давления.
Обозначим ее через q
q=s₀/ bt1, тогда х=P/q
Если при возрастании давлении P=q, то х=1. Это значит, что N(q) таково, что N(q)t₁=s₀ - число молекул на единицу площади.
Если адсорбция происходит на свободной поверхности, то второй, третий и последующие слои заполняются целиком, адсорбируя s₀ молекул на единицу поверхности Ю s ® Ґ, что не трудно видеть, подставив вместо "х" - "1".

Подставив х =P/q, получим
 s = кРs₀ /((q-P)[1+(к-1)P/q)])      (11)
Уравнение содержит три постоянные к, q, s₀.
Величину s₀ можно оценить из размеров молекул или из размеров адсорбционных "центров" поверхности в случае "неподвижной" адсорбции.
Экспериментально измеренное общее число адсорбированных молекул пропорционально( ~ ) общей площади поверхности адсорбента S.
 Измеряемая величина представляет собой произведение sS.
Если измеряемые в опыте величины получены в объемах адсорбированного газа
( v ~ sS), то уравнение примет вид

v = кРv_m /((q-P)[1+(к-1)P/q)]),
где v_m- объем адсорбированного газа, когда вся поверхность адсорбента покрыта монослоем.
 Если величины к, q, Jm рассчитаны графически по экспериментальным данным, то значение v_mявляется прямой мерой величины поверхности образца S.
 Брунауэр, Эммет и Теллер отождествили J с Ро - давлением насыщенных паров адсорбирующегося вещества при Т опыта. Это допущение означает, что на графике зависимости v от Р/Ро v®Ґ при Р/Ро®1.
Уравнение изотермы v = кРv_m/((Ро-P)[1+(к-1)Р/Ро)]).
Тогда данное уравнение можно записать в виде
Р/(v(Ро-P)) = 1/(v_mк)+(к-1)/(v_mк) Ч Р/Ро
(график левой части от Р/Ро дает прямую).
 Согласно этому упрощению, мы должны принять, что теплота адсорбции и вероятность испарения молекул, расположенных поверх слоя адсорбированных молекул, равны соответственно теплоте испарения и вероятности испарения из той же жидкости. Учитывая это в нашем выводе, подставим

к=t/t₁= (t₀ exp(Qa/RT))/((t₀)1 exp(Q1/RT))
t₀ = (t₀)1 и Q1=Qо, т.е. скрытой теплоте испарения адсорбции вещества в жидкой фазе. Тогда к = ехр((Qa-Qo)/RT) (12).
Из графика можно найти v_mи к, а затем S(величину поверхности и теплоту адсорбции первого слоя Qa, если известна скрытая теплота испарения Qo.
 Рассмотрим теперь поподробнее выведенное уравнение.

Обозначим s/s₀=J, тогда J =кх/((1-x)(1-х+кх)) (*).
Если в уравнении Лэнгмюра J<1, то в случае полимолекулярной адсорбции следует иметь в виду, что s может быть >s₀. Поэтому теоретически J может принимать любые значения от 0 до Ґ. Если х << 1, то J=кх/(1+кх), при условии, что "к" достаточно велико, чтобы кх не было мало по сравнению с единицей. Уравнение (*) представляет собой уравнение Лэнгмюра, т.к. к=t/t₁ и х=P/J=Pbt1/s₀.
Тогда кх=t/t₁ Ч Pbt1/s₀=t₁/s₀ Ч bP.

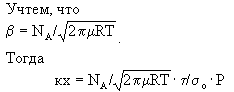
  Таким образом, для небольших P/J уравнение (*) переходит в уравнение изотермы Лэнгмюра.
 Если 0,5ЈхЈ1, а кх>>(1-х), то J=1/(1-х).
(Следует отметить, что значения Р, q, t и t₁ или температуры не оказывают существенного влияния на форму изотермы, построенной в координатах J-P/Pо.)
{ГРАФИКИ}
а),б) - домонослойное покрытие, описываемое изотермой Лэнгмюра.

в) - полимолекулярная адсорбция.