Рассмотрим более подробно связь между напряжением на затворе V_G МДП структуры и поверхностным потенциалом Y_s. Все приложенное напряжение V_G к МДП структуре делится между диэлектриком и полупроводником, причем очевидно, что падение напряжения в полупроводнике равняется поверхностному потенциалу Y_s. Таким образом,

V_G =V_ox+Y_s   (1).

Из (1) и анализа зонных энергетических диаграмм на рисунке следует, что знак поверхностного потенциала Y_s, выбранный нами ранее a priori, в действительности соответствует знаку напряжения на затворе V_G. Действительно, положительное напряжение на затворе идеальной МДП структуры вызывает изгиб зон вниз у полупроводников n и p-тирпа, что соответствует положительным значениям поверхностного потенциала. Отрицательное напряжение V_G вызывает изгиб зон вверх у поверхности полупроводника, что соответствует отрицательному значению поверхностного потенциала Y_s.

Из условия электронейтральности следует, что заряд на металлическом электроде Q_m должен быть равным суммарному заряду в ОПЗ Q_sc , заряду поверхностных состояний на границе раздепа полупроводник-диэлектрик Q
ss и встроенному заряду в диэлектрик вблизи границы раздела Q_ox. Тогда

-Q_m=Q_ss+Q_sc+ Q_ox.

Согласно определению геометрической емкости Co

C_ox=Q_m/V_ox,

отсюда  V_ox=-Q_ss/C_ox - Q_sc/C_ox - Q_ox/C_ox.

Учитывая, что между металлом и полупроводником существует разность термодинамических работ DY_ms, получаем
  V_G= -DY_ms  - Q_ox/C_ox+qN_ssY₀/C_ox+Y_s-Q_ss/C_ox+qN_ssY_s/C_ox (2).
 Введем новое обозначение - напряжение плоских зон V_fb (flat band). Напряжением плоских зон V_fb называется напряжение на затворе реальной МДП структуры, соответствующее значению поверхностного потенциала, равного нулю V_fb=V_G(Y_s=0) (3).

С учетом определения (2) из (3) следует
V_fb =DY_ms  - Q_ox/C_ox+qN_ssY₀/C_ox (4).
 Таким образом связь между напряжением на затворе V_G и поверхностным потенциалом Y_s с учетом (4) задается в виде

V_G=V_fb+Y_s+qN_ssY_s/C_ox- Q_sc/C_ox  (5).

 Проведем более подробный анализ (5) для различных областей изменения поверхностного потенциала (Y_s).
 Обогащение (Y_s<0).
 .
При обогащении поверхности дырками, как основными носителями поверхностный потенциал Y_s зависит от напряжения на затворе V_G логарифмически, а заряд Q_sc  в ОПЗ зависит от напряжения на затворе V_G линейно.

Обеднение и слабая инверсия (0<Y_s<2j0 ).
 Заряд в ОПЗ Q_sc в этом  случае в основном обусловлен ионизованными акцепторами Q_B.
  V_G -V_fb=nY_s   (6),
где  n=1+qN_ss/C_ox +C_B*/C_ox.
Здесь Q_B*, C_B*- величина заряда и емкости ионизованных акцепторов в ОПЗ при Y_s=y0.
 Из соотношения (6) следует, что в области обеднения и слабой инверсии поверхностный потенциал
зависит от напряжения V_G линейно, причем tga=dV_G/dY_s=n определяется плотностью поверхностных состояний N
ss, толщиной подзатворного  диэлектрика d0x и уровнем легирования полупроводниковой подложки NA.

Сильная инверсия (Y_s>2j0).
Заряд в ОПЗ Q_sc отрицателен, состоит из заряда ионизованных акцепторов Q_B и электронов Qn в инверсионном слое.
 Введем пороговое напряжение Vt как напряжение на затворе V_G, когда в равновесных условиях поверхностный потенциал Y_s равен пороговому значению 2j0.

.
Vt=V_fb+2j0- Q_B/C_ox+2qN_ssjo/C_ox  (7).

Из (7) следует, что если отсчитывать пороговое напряжение VT от напряжения плоских зон V_fb, то оно будет состоять из падения напряжения в полупроводнике 2j0 и падения напряжения на подзатворном диэлектрике за счет заряда ионизованных акцепторов и заряда в поверхностных состояниях. Для достаточно высоких значений Y_s, когда bDY_s>1, имеем

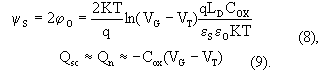
Из (8) и (9) следует, что в области сильной инверсии, так же как и в области обогащения, поверхностный потенциал логарифмически зависит от напряжения на затворе V_G, а заряд электронов в инверсионном слое Qn линейно зависит от величины V_G.

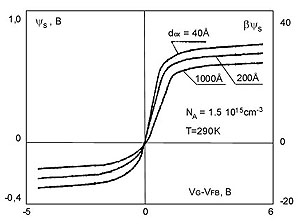
На рисунке приведена зависимость поверхностного потенциала Y_s от напряжения на затворе V_G, рассчитанная для различных толщин подзатворного диэлектрика dox.