Функция распределения Ферми-Дирака
Распределение электронов и дырок по энергиям в
твердом теле описывается статистикой Ферми-Дирака.
Согласно этой статистике вероятность того, что состояние с некоторой
энергией E при температуре Т будет занято электроном,
определяется функцией Ферми-Дирака: (fo)
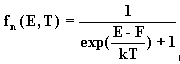 (1)
(1)
Вероятность нахождения на этом уровне дырки будет соответственно:
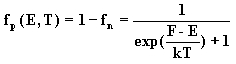 k - постоянная Больцмана
Т - абсолютная температура
F-энергия Ферми, т.е. работа, которую необходимо
затратить для изменения числа частиц в системе на единицу.
Рассмотрим вид функции Ферми-Дирака
при различных температурах:
k - постоянная Больцмана
Т - абсолютная температура
F-энергия Ферми, т.е. работа, которую необходимо
затратить для изменения числа частиц в системе на единицу.
Рассмотрим вид функции Ферми-Дирака
при различных температурах:
ПОСМОТРЕТЬ АНИМАЦИЮ 
Из (1) следует, что в случае Т=0 в интервале
энергии 0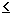 Е<F
имеем fo =1 и fo=0 для Е>F. Это означает, что все квантовые состояния
с энергией, меньшей энергии Ферми, заняты электронами, а уровни, лежащие
выше уровня Ферми, полностью свободны. Следовательно,
энергия Ферми есть максимально возможная энергия электронов при температуре
абсолютного нуля.
Е<F
имеем fo =1 и fo=0 для Е>F. Это означает, что все квантовые состояния
с энергией, меньшей энергии Ферми, заняты электронами, а уровни, лежащие
выше уровня Ферми, полностью свободны. Следовательно,
энергия Ферми есть максимально возможная энергия электронов при температуре
абсолютного нуля.
Рассмотрим случай, когда T>0. Из выражения
(1) для значения энергии E=F имеем fo=1/2. Таким образом, уровень
Ферми есть энергетический уровень, вероятность заполнения которого при
температуре T>0 равна 0,5.
Произведем оценку области изменения функции
распределения fo (Е) для случая T>0. Для этого подсчитаем значение fo (Е)
для разных значений энергии. Для энергий, отличающихся от F на ±kT, значение
fo (Е) составляет 1/(1+e)=0,27 и 1/(1+1/e)=0,73.
При изменении энергии на ±2kT значение
fo (Е) равно 0,118 и 0,882, а при изменении на ±3kT значение fo (Е)
равно 0,047 и 0,953. Из этих данных следует, что вероятность
заполнения состояний заметно отличается от единицы или нуля лишь в пределах
(2-3)kT вблизи значения E=F.
Для электронов, находящихся в состояниях с
энергией E-F »kT, выражение (1) принимает вид:
fo (Е) =exp[(F-E)/kT]=Cexp(-E/kT), т.е. совпадает с функцией
распределения Максвелла-Больцмана. Если носители
заряда подчиняются статистике Больцмана, то полупроводник называется невырожденным.