
 |
Физические сигналы являются непрерывными
функциями времени. Чтобы преобразовать непрерывный, в частности, аналоговый
сигнал в цифровую
форму используются аналого-цифровые пребразователи (АЦП). Процедуру аналого-цифрового
преобразования сигнала обычно представляют в виде последовательности
трех операций: дискретизации,
квантования и кодирования. Операция дискретизации заключается
в определении выборки моментов времени измерения сигнала. |
Операция квантования состоит в считывании значений координаты сигнала в выбранные моменты измерения с заданным уровнем точности, а операция кодирования - в преобразовании полученных измерений сигнала в соответствующие значения некоторого цифрового кода или кодовой комбинации, которые затем передаются по каналам связи.
Процедуру восстановления непрерывного сигнала из цифрового представления также можно представить в виде двух операций: декодирования и демодуляции. Операция декодирования выполняет операцию обратную операции кодирования, т.е. преобразует последовательность заданных значений кодовой комбинации (кодовых слов) в последовательность измерений, следующих друг за другом через заданные интервалы времени дискретизации. Операция демодуляции выполняет интерполяцию или восстановление непрерывного сигнала по его измерениям. Преобразование сигнала из цифровой формы в непрерывный сигнал осуществляется цифро-аналоговыми пребразователями (ЦАП). Считается, что система аналого-цифрового и цифро-аналогового преобразований адекватна сигналу, если восстановленный непрерывный сигнал (копия) соответствует исходному непрерывному сигналу (оригиналу) с заданной погрешностью.
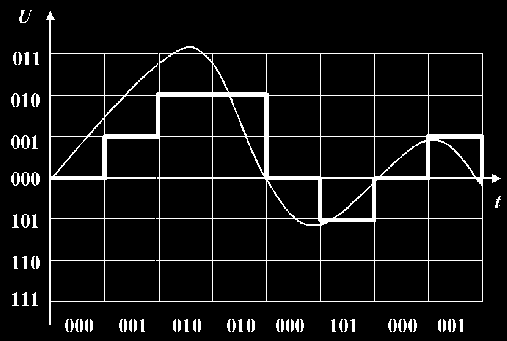
При квантовании по уровню непрерывное множество значений функции x(t) заменяется множеством дискретных значений. Для этого в диапазоне непрерывных значений функции x(t) выбирается конечное число дискретных значений этой функции (дискретных уровней) и в процессе квантования значение функции x(t) в каждый момент времени заменяется ближайшим дискретным значением. В результате квантования образуется ступенчатая функция g(t).
Квантование по уровню практически может осуществляться двумя
способами. При первом способе квантования мгновенное значение функции x(t)
заменяется меньшим дискретным значением. При втором способе квантования
мгновенное значение функции x(t) заменяется ближайшим меньшим или большим
дискретным значением в зависимости от того, какое из этих значений ближе
к мгновенному значению функции.В этом
случае переход ступенчатой функции с одной ступени на другую происходит в те
моменты, когда первоначальная непрерывная функция x(t) пересекает середину
между соответствующими соседними дискретными уровнями. |
 |
Расстояние между дискретными соседними уровнями называется интервалом или шагом квантования. Различают равномерное квантование по уровню, при котором шаг квантования постоянен, и неравномерное квантование по уровню, когда шаг квантования непостоянен. На практике преимущественное применение получило равномерное квантование в связи с простотой его технической реализации.
Вследствии квантования функции по уровню появляются методические погрешности, так как действительное мгновенное значение функции заменяется дискретным значением. Эта погрешность, которая получила название погрешности квантования пол уровню или шума квантования, имеет случайный характер. Абсолютное её значение в каждый момент времени определяется разностью между квантованным значением g(t) и действенным мгновенным значением x(t) функции. Закон распределения этой погрешности зависит от закона распределения x(t).
Рассмотрим сущность понятия дискретизации сигнала x(t) применительно к детерминированной
функции. Дискретизация сигнала x(t) связана с заменой промежутка изменения
независимой пременной некоторым множеством точек, т.е. операции дискретизации
соответствует
отображение x(t) x(ti)
x(t) – функция, описывающая сигнал
x(ti) – функция, описывающая сигнал, полученный в результате дискретизации,
то есть в результате дискретизации исходная функция x(t) заменяется совокупностью
отдельных значений x(ti). По значениям x(ti) можно восстановить исходную функцию
x(t) с некоторой погрешностью. Функция, полученная в результате восстановления
(интерполяции) по значениям x(ti) , называется воспроизводящей и обозначается
через V(t).
При обработке сигналов дискретизация по t должна производится таким образом, чтобы по отсчетным значениям x(ti) можно было получить воспроизводящую функцию V(t), которая с заданной точностью отображает исходную функцию x(t). При дискретизации сигналов приходится решать вопрос о том, каков должен быть шаг дискретизации=ti-ti-1.
При малых шагах дискретизации количество отсчетов функции на отрезке обработки
будет большим и точность воспроизведения – высокой. При больших количество
отсчетов уменьшается, но при этом снижается точность восстановления. Оптимальной
является такая дискретизация, которая обеспечивает представление исходного
сигнала с заданной точностью при минимальном количестве выборок.
В этом случае все отсчеты существенны для восстановления исходного сигнала.
При неоптимальной дискретизации имеются еще и избыточные отсчеты, которые
не нужны для восстановления сигнала с заданной точностью и загружают канал
передачи
информации. Задача сокращения избыточных отсчетов может рассматриваться как
задача описания непрерывных сигналов с заданной точностью минимальным чмслом
дискретных характеристик.
| Аналогово-цифровое преобразование |