14.2.5. Ток туннельной инжекции через трапециидальный барьер

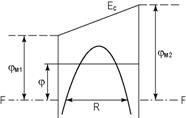
Для барьера трапециидальной формы, а также при учете сил зеркального изображения форма барьера усложняется. Выражение для инжекционного туннельного тока сквозь потенциальный барьер произвольной формы имеет следующий вид (рис. 14.16).

 

Рис. 14.16. Туннелирование через потенциальный барьер произвольной формы

 

,

(14.66)

где  – средняя высота барьера (если барьер произвольной формы заменить прямоугольным барьером той же самой площади), R – расстояние туннелирования, т. е. ширина барьера на уровне Ферми электрода. Формула (14.66) является приближенной, но дает достаточно точные для практических расчетов результаты. Величины a и b в формуле (14.66) постоянные

.

(14.67)

Проверим точность формулы (14.66) для треугольного барьера без учета сил изображения. Высота барьера со стороны электрода, из которого идет эмиссия электронов, равна φ_н. Средняя высота треугольного барьера . Расстояние туннелирования (ширина барьера) .

Рассмотрим туннелирование через трапециидальный барьер. На рис. 14.4 показано, как меняется форма трапециидального барьера при малой толщине диэлектрического слоя, когда надо учитывать силы изображения электрона на левом и правом контактах. Если толщина слоя превышает 5 нм, то потенциальный барьер будет мало отличаться от трапециидального. Средняя высота такого барьера . Расстояние туннелирования равно толщине диэлектрического слоя R = d. Тогда из формулы (14.66) для трапециидального барьера получим

,

(14.68)

где

.

(14.69)

Уравнение (14.68) дает зависимость туннельного инжекционного тока от напряженности поля в диэлектрическом слое E_c.
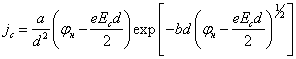