---

Рентгеноструктурный анализ аморфных материалов

---

4.1. Ошибка, возникающая из-за обрыва кривой распределения интенсивности рассеяния

Эффект обрыва является серьезной проблемой Фурье-преобразования кривой распределения интенсивности. Анализ влияния обрыва на D(r ) проведен в целом ряде работ [5,6,35-37 ] . Показано, что обрыв вызывает размытие и смещение максимумов функции радиального распределения и появление ложных пиков около каждого максимума на расстояниях r = r_ij ±2,5 π/K _m , где K_m - максимальное значение модуля дифракционного вектора, до которого получены экспериментальные данные. При уменьшении K_m наблюдается также ухудшение разрешения кривой D(r ). На рис.23 приведены кривые D(r ) для окислов Та ₂O₅, Nb₂O₅ и W О ₃ , рассчитанные для различных значений K_m.

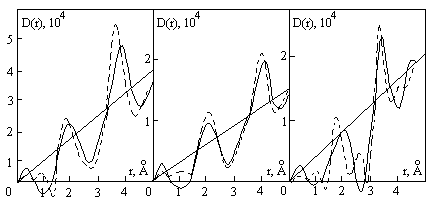
Рис. 23. Кривые D(r ) для окислов :

a - Та ₂O₅; ---K_m=17 A^{o –1} ; ― K _m = 4,2 A^{o –1};

б - Nb₂O₅; ---K_m=7,75 A^{o –1} ; ― K _m = 4,2 A^{o –1};

в - W О ₃; ---K_m=17 A^{o –1} ; ― K _m = 5,6 A^{o –1};

Видно, что для окислов Та ₂O₅ и Nb₂O₅ уменьшение K_m приводит только к размыванию и смещению пиков на D(r ). На кривой D(r ) для W О ₃ имеет место ухудшение разрешения с уменьшением K_m до 5,6 A^{o -1} . Такое поведение D(r ) объясняется тем, что для Та ₂O₅ и Nb₂O₅ функция Н(К) носит резко выраженный затухающий характер : после К=10 A^{o -1} осцилляций практически нет (рис. 24а). В случае W О ₃ осцилляции кривой Н(К) относительно нуля уменьшаются по амплитуде гораздо медленнее (рис. 246).

Рис. 24. Функция H(K) для а - W О ₃ ; б - Та ₂O₅

Причина кроется в различной дальности корреляции в расположении атомов в этих окислах : чем медленнее приближается рассеяние аморфным материалом к независимому рассеянию, тем больше размер области ближнего упорядочения. Известно, что наиболее заметное влияние обрыв экспериментальных данных оказывает на значение первого координационного числа. Поведение ошибки обрыва иллюстрирует рис.25, на котором приведена характерная кривая ∆ D _к (r)=(D _{к1 m}(r)- D _{к2 m}(r )) равная разности D(r ), рассчитанных при двух значениях К _m: К _m1 и К _m2. К _m - максимальное значение модуля дифракционного, вектора, для которого получена данная кривая D _{к m}(r ). Максимальные амплитуды осцилляций обрыва имеют место в области 2 ÷ 4 A^o , то есть в области наибольшей информативности кривой D(r).

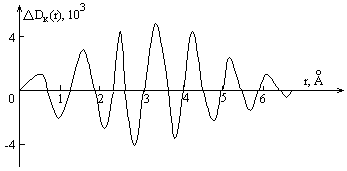
Рис.25. Кривая Δ D _к (r ), иллюстрирующая поведение ошибки обрыва

Влияние обрыва данных на значения радиусов координационных сфер и координационного числа в общем случае непредсказуемо. Для исключения его можно воспользоваться методами, рассмотренными в работах [35-37] в применении к одноатомным материалам. Первый [35] заключается в проведении последовательной корректировки кривой G(r)=4π(ρ(r)-ρ _o) путем выявления характера поведения ошибки обрыва кривой i( К ) при различных значениях К _m . Исправляя G(r ) на эту ошибку, используют два критерия правильности метода:

1) при отсутствии иных ошибок кривая G(r ), исправленная на обрыв в области до первого максимума, должна быть линейной функцией r;

2) полученная из исправленной G(r ) методом обратного Фурье-преобразования функция i (К) должна совпадать с экспериментальной.

Последовательными приближениями авторам работы [35] удалось

получить корректные данные для жидкой ртути и свинца. Метод, рассмотренный в работе [37 ] , разработан только для одноатомных материалов.

В уравнении (2.23) обозначим 4π(ρ(r)-ρ _o ) через G(r ) тогда

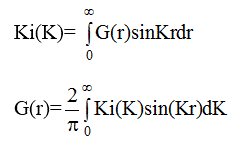(4.1)

На практике обычно вводится демпферный множитель ехр( -α ² К ²) для уменьшения влияния пиков обрыва на G(r ) и для уменьшения влияния ошибок в значениях i(K) полученных в области больших К, так что из эксперимента имеем функцию G _э (r ), равную

(4.2)

Из (4.1) и (4.2) получим

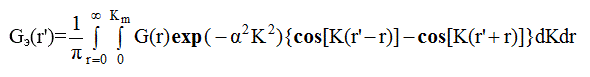
Определим функцию обрыва g( ε ) как

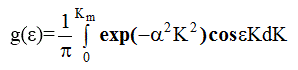
Условие нормировки имеет вид :

Тогда

Для дальнейших расчетов удобно ввести функцию G(-r)= -G(r ) так, что если r= -х, то

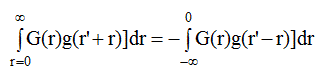
то есть

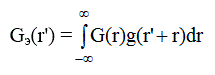(4.3)

Мы получили G _э (r ) в виде свертки истинной функции G(r ) и функции обрыва g( R-r), или

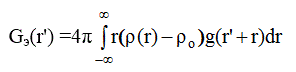
Введя обозначения: F _э (r')= G _э (r')+4πr'ρ _o, а F(r)= 4πrρ _o, получим уравнение, связывающее искомую величину F(r) с экспериментально полученной F _э (r'):

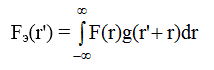
Уоррен [37] показал, что функцию обрыва g(r - r') можно записать в виде :

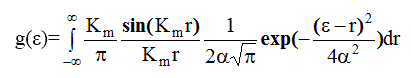
то есть g( ε ) является сверткой двух функций :

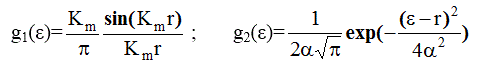
Отсюда F _э (R ) может быть представлена в виде двойной свертки:

Fэ(r') = F(r)*g₁(r)*g₂(r) (4.4)

Однако, когда одной из функций оказывается искомую функцию F(r ) невозможно получить путем обратной свертки, используя один из стандартных методов (метод последовательных сверток, моментов или преобразования Фурье). Поскольку реальная функция F(r ) представляет собой обычно несколько острых пиков, накладывающихся на медленно изменяющийся фон , то можно использовать для получения F(r ) приближенный метод, основанный на том, что острые пики на F(r ) заменяются гауссовыми, а сверткой с медленно изменяющимся фоном пренебрегают.

Для каждого из пиков можно получить функцию f_i(r_i):

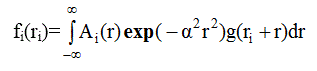
где i - номер максимума. Коэффициенты А _i и α подбираются для каждого пика F _э (R) исходя из того, что высота и полуширина f_i(R_i ) и соответствующего максимума на F _э (r) должны совпадать.

Далее рассчитывается функция F’(r)

(4.5)

Несмотря на приближенность функции F’(r) , она ближе к истинной F(r) , чем к F _э (r) , и влияние обрыва данных практически исключено.

Есть, тем не менее, некоторая неоднозначность в рассматриваемой методике, связанная с тем, что даже в однокомпонентных материалах второй, а тем более третий максимум на F _э (r) является результатом наложения двух, а иногда и более координационных сфер. В многоатомных материалах все усложняется еще и тем, что перекрывающиеся пики отвечают сферам, на которых находятся атомы разного сорта.

Применение метода парных функций практически полностью снимает проблемы учета влияния обрыва на характеристики ближнего упорядочения. Представление кривой D(r ) в виде суммы парных функций (см. раздел 2.5.2) и расчет N_ij МНК с учетом осцилляций обрыва, отвечающих каждому максимуму, приводит к тому, что значения N_ij, r_ij и σ _ij начиная с какого-то конкретного для данного материала значения К _m , не зависят от верхнего предела интегрирования в формуле (2.76). Иллюстрирующие данный вывод расчеты приведены в таблице 7.

Таблица 7.

Радиус первой координационной сферы, первое координационное число и размытие сферы, рассчитанные из D(r ), полученных при различных верхних пределах интегрирования

Вещество	Km Å-1	4,2	Km = 5,6	Km = 7,8	Km = 10	Km = 12	Km = 15	Km = 17
Ta2O5	r1, Ao N1, а.т. σ 1, Ao	1,98 7,6 0,14	1,97 7,5 0,14	1,99 7,6 0,14	1,98 7,6 0,14		1,97 7,4 0,14	1,97 7,5 0,14
Nb2O5	r1, Ao N1, а.т. σ 1, Ao	1,97 7,05 0,21	1,98 7,0 0,18	1,98 7,1 0,18
WO3	r1, Ao N1, а.т. σ 1, Ao		1,88 6,0 0,07	1,88 5,8 0,07	1,88 5,0 0,10	1,88 5,0 0,10	1,88 5,0 0,10	1,88 5,0 0,10

Из таблицы 7 видно, что для Ta₂O₅ и Nb₂O₅ в пределах погрешности экспериментальных данных нет зависимости N ₁, r₁ и σ ₁ от К _m . Для WO₃ указанные параметры стабилизируются, начиная с К _m = 10 Å.

Кроме того, пики на кривой D _мнк (r ) в области до первого максимума соответствуют только обрыву данных. Отсутствие совпадения D(r ) и D _мнк (r ) в этом интервале r свидетельствует о наличии в кривых D(r ) ошибок эксперимента и расчета, не связанных с обрывом. Построение разности D(r)-D _мнк (r ) помогает диагностировать тип имеющееся в D(r ) погрешности. Для этого необходимо промоделировать различные возможные ошибки.

Далее.

Содержание Главы 4.

Содержание.