---

Рентгеноструктурный анализ аморфных материалов

---

2.5.2. Метод Финбака

Более точный метод обработки результатов эксперимента для рассматриваемых в данном разделе объектов был разработан норвежской школой Финбака и изложен в монографии Уоррена [10].

В исходной формуле для интенсивности рассеяния многокомпонентной системой рассеивающих центров (2.44) необходимо провести усреднение по ориентациям относительно вектора , так рассмотрение ограничивается изотропными объектами. Для таких материалов авторы [10] ввели функцию как число атомов в объеме на расстоянии от атома m , умноженное на функцию атомного рассеяния f_n. Поскольку рассматриваются изотропные объекты, функция будет сферически симметричная, то есть . Тогда среднее по всему рассеивающему объему значение будет равно

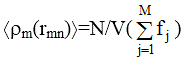
Добавив и вычтя последнее из сумму по n в (2.44) заменили интегралом по объему образца:

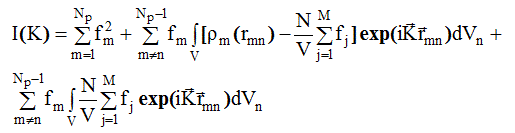(2.58)

Величина не зависит от направления вектора , а определяется только величиной модуля последнего. Это означает, что любые ориентации вектора относительно дифракционного вектора равновероятны и экспоненту в формуле (2.5 8 ) можно усреднять по ориентация вектора относительно направления вектора К. Тогда среднее значение экспоненты:

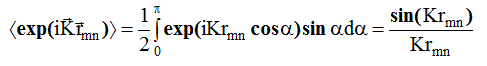
Выражение (2.58) примет вид:

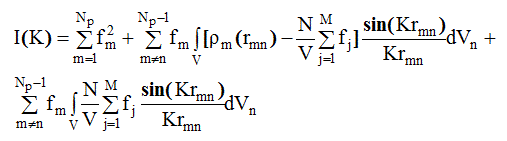(2.59)

Ниже мы покажем, что последнее слагаемое в формуле (2.59) имеет заметные значения только в области очень малых углов, то есть, описывает мало угловое рассеяние рентгеновских лучей данной системой рассеивающих центров, поэтому при записи дальнейших формул это слагаемое опускается. Функция вводилась только для обоснования усреднения экспоненты. Вернувшись вновь к суммированию по n получим:

(2.6)

Мы рассматриваем скопление из N одинаковых групп, в каждой из которых n_о атомов. Будем вновь в одну группу объединять атомы, образующие единицу состава, и, учитывая хаотичность ориентации групп, заменим в (2.60) суммирование по m на суммирование по единице состава, обозначив его . Кроме того, сумму по n удобно заменить на сумму по координационным сферам, вводя N_ij как среднее число атомов на i- й сфере, имеющей радиус r_ij и центр в атоме j . И, наконец, пусть q_m(r ) - часть поверхности сферы радиуса r , имеющей центр в атоме m , находящаяся в пределах рассеивающего объема образца. Учитывая все вышесказанное и заменив dV_n на 4 p r²q_m(r)dr , имеем из (2. 60):

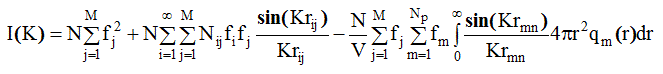(2.61)

Интегрирование в последнем слагаемом производится до , поскольку, по определению, при r , больших, чем размер рассеивающего объема. Пусть - среднее значение по всем m атомам образца, тогда q(r) =1 при r =0 и при больших r . Введя q(r ) в (2.61), после некоторых перестановок получим.

(2.62)

Записав интерференционную функцию рассеяния как

(2.63)

и обозначив через Y(K) интеграл

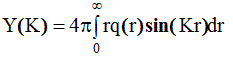(2.64)

домножим обе части выражения (2.62) на на произведение g^-2(K)exp(-α²K²)sin(Kr) и проинтегрируем по K от 0 до K_m.

(2.65)

Множитель exp(-α²K²) представляет собой фактор затухания, который вводится для уменьшения влияния ошибок в значениях интенсивности, регистрируемых в эксперименте при больших углах рассеяния. Функция g(K) - это коэффициент заострения, обуславливающий повышение контрастности интерференционной картины при больших значениях длины дифракционного вектора K. Коэффициент заострения g(K) выбирается так, что g(K)≈1 при K = 0 и уменьшалосьс возрастанием K. Чаще всего g(K) выбирают равным fe (см. формулу 2.45).

Покажем, что Y (К) пренебрежимо мало при всех значениях К за исключением очень малых. Проведем для этого в (2.64} ряд последовательных интегрирований по частям. Правило интегрирования по частям записывается в виде :

Если , а , то и .

Тогда

Первое слагаемое обращается в нуль, так как при r=0 Sin(Kr)=0 и rCos=0 , а при q(r)=0. При повторном интегрировании

, ,

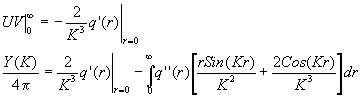
Продолжая аналогичным способом интегрирование дальше, получим

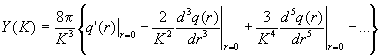
Очевидно, что Y (К) быстро уменьшается с ростом длины дифракционного вектора К, то есть последнее слагаемое формулы (2.59) действительно имеет заметные значения лишь при К, близких к нулю, и представляет собой I _мур(K).Как следствие, в последнем слагаемом формулы (2.65) верхний предел интегрирования можно заменить на бесконечность и все медленно изменяющиеся величины на их значе-ния при K = 0. Получаем

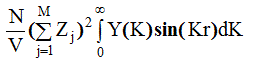
Из (2.64) следует, что Y (К) - Фурье-трансформанта функции rq(r ). Обратное Фурье-преобразование дает

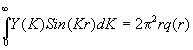
Отсюда последнее слагаемое уравнения (2.65) принимает вид:

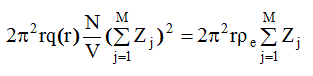
поскольку для используемых значений r q(r)=1 (так как r << размера облучаемого объема), p _e - электронная плотность вещества. С учетом этого уравнение ( 2. 65) перепишем в виде:

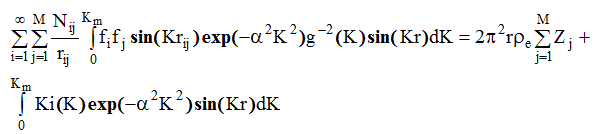(2.66)

Теперь удобно ввести ряд парных функций P_ij(r):

(2.67)

Функция P_ij(r ) описывает распределение электронной плотности одной отдельно взятой пары атомов, имеющей межатомное расстояние r_ij , и называется парной функцией. В окончательной форме уравнение (2.66) можно записать так:

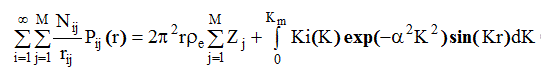(2.68)

Правая часть рассчитывается из экспериментальных интенсивностей I (К), обозначается обычно D(r ) и имеет вид , представленный на рис.8.

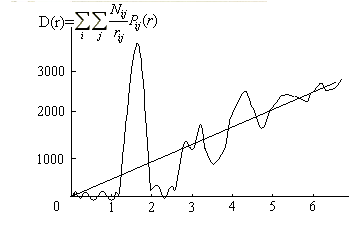
Рис. 8. Кривая распределения парных функций D(r ) для SiO₂ [11]

Положения пиков дают соответствующие межатомные расстояния . Анализируя набор полученных межатомных расстояний, можно идентифицировать тип атомов, находящихся на данном расстоянии, и рассчитать для каждого r_ij свою парную функцию P_ij(r ) по формуле (2.67) . Подставив значения P_ij(r), r_ij и D(r ) в (2.68), получим систему уравнений , линейную относительно значений Nij . Число уравнений определяется числом точек на кривой D (r ), число неизвестных - количеством координационных сфер, для которых производится расчет.

Нужно заметить, что P_ij(r ) рассчитывается с использованием тех же значений g( К) и е xp(- a ² К ²) , которые выбираются при расчете D( r ) из К _i (К). Для удобства проведения расчетов и наглядности анализа поведения функций P_ij(r ) авторы работы [13] представили парную функцию в виде суммы двух слагаемых вида:

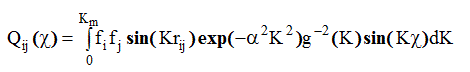( 2.69)

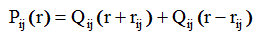(2.70)

Функция Q_ij(r - r_ij) симметрична относительно r_ij, и не зависит от величины r_ij . Вклад второго слагаемого Q_ij(r + r_ij) , обуславливающего как некоторую асимметрию P_ij(r ) около r_ij , так и зависимость P_ij(r ) от r_ij , авторы работ [10-14] считают незначительным и пренебрегают им при дальнейших расчетах .

На рис.9 представлены кривые P_ij(r)=Q_ij(r - r_ij), a=0,056, K _m=21,1 A^{0 -1};g(K)=f_e(K) [13].

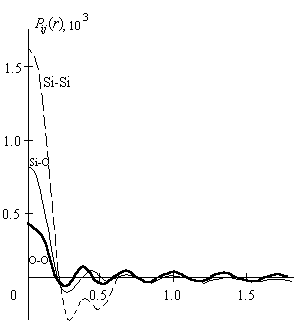
Рис.9. Кривые распределения P_ij(r)=Q_ij(r - r_ij) для различных пар атомов [6].

Следует подчеркнуть, что в рассматриваемой ситуации отсутствие зависимости P_ij(r ) от r_ij обуславливает тот факт, что парные функции теперь зависят только от сорта атомов, образующих пару. Это означает, что в двухатомной системе необходимо рассчитывать только три функции P_ij(r ), которые и показаны на рис.9. Каждая парная функция в этом случае симметрична относительно c =0 , где χ = r - r_ij . Сопровождающие основной максимум сателлиты представляют собой пики обрыва. Как ширина центрального основного максимума кривой P_ij(r), так и амплитуда и ширина сателлитов обрыва определяются величиной верхнего предела интегрирования в формулах (2.67) и ( 2.68).

Тождественность значений K_m в обеих вышеуказанный формулах обеспечивает возможность надежного исключения влияния обрыва экспериментальных данных на значения r_ij и N _ij , определяемые из кривых D(r).

В реальных некристаллических материалах ширина (максимумов функции P_ij(r) ( или P_ij(r)) возрастает вследствие наличия дисперсии σ_ij межатомных расстояний относительно среднего значения r_ij , определяемого положением соответствующего максимума на D(r ). Величина σ_ij частично обусловлена тепловыми колебаниями атомов. Если обозначить функцию распределения расстояний через G_ij(r_ij ), то эффективную парную функцию P_ij( r) можно получить сверткой P_ij(r) и G_ij(r_ij),

(2.71)

Обычно используют различные пробные функции G_ij(r_ij ), подбирая такую, которая наилучшим образом описывает форму максимумов кривой D(r ). В работах [13,14] использовалась простейшая функция G_ij(r_ij ), имеющая форму треугольника. В [12 ] была выбрана функция Гаусса:

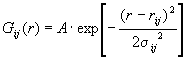(2.72)

Коэффициент нормировки А должен быть таким, чтобы площади под P_ij( r) и P_ij‘( r) были равны.

Если следовать Уоррену, то есть считать, что P_ij(r)=Q_ij(r - r_ij) , то интеграл в формуле (2.71) можно вычислить аналитически и тогда

(2.73)

Можно вывести простое выражение для площади под парной функцией. Введен в формулу (2.67) под знаком интеграла коэффициент U(K ) такой, что U(K) = 1 при и U (К) = 0 при К > К _m . Тогда верхний предел интегрирования можно увеличить до ∞ и с помощью Фурье - преобразования можно получить

Для очень малых К заменим все медленно изменяющиеся величины на их значения при К= 0. Тогда

Считая, что P_ij(r ) симметрична относительно r_ij, имеем

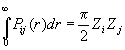(2.74)

На практике этот простой результат должен использоваться с осторожностью: необходимо учитывать, что значительную часть площади могут составить сателлиты, или "крылья", парной функции.

С учетом размытия координационных сфер уравнение (2.66) можно привести к виду;

(2.75)

где, как указывалось выше,

(2.76)

Значения D(r ) в каждой точке r рассчитываются из экспериментально полученной функции , выраженной в электронных единицах на единицу состава.

Таким образом, мы имеем систему из n₁ уравнений, где - число точек на кривой D(r ). Неизвестными величинами в системе являются N_ij, r_ij и σ _ij . Задавая значения r_ij и σ_ij , координационные числа N_ij можно найти методом наименьших квадратов (МНК) [1 2],

В первом приближении радиусы координационных сфер r_ij и их размытия σ_ij обычно задаются как положения и размытия соответствующих максимумов кривой распределения D(r). Уточнение значений r_ij и σ_ij проводится методом последовательных приближений. Необходимость такого уточнения обусловлена влиянием обрыва экспериментальных данных на положения пиков на D(r) и невозможностью точного нахождения σ_ij непосредственно из экспериментальной кривой. Окончательные значения N_ij, r_ij и σ_ij от величины K_m не зависят. Однако такой подход, как правило, однозначно позволяет определить только первое координационное число, поскольку для основной массы некристаллических материалов лишь первый максимум кривой D(r) достаточно хорошо разрешен и определяет число ближайших соседей и расстояние между ними. Во второй максимум обычно вносят вклад пары атомов разного сорта (рис. 8).

В связи с этим во втором приближении задаются в качестве исходных данных значения N_ij, r_ij и σ_ij (начиная с i=2 ), рассчитанные для той кристаллической модификации исследуемого материала, для которой первое координационное число и радиус первой сферы близки к значениям r₁ и N₁, рассчитанным в первом приближении из D(r) . Если имеется ряд модификаций с одинаковыми N₁ и близкими r₁ , то расчеты целесообразно производить для каждой из них. σ _ij при этом необходимо подбирать методом последовательных приближений, минимизируя разность между кривыми D(r) и D _к (r).

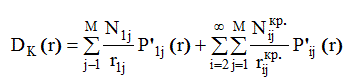
N_ij ^кр , r_ij ^кр - значения N_ij и r_ij для соответствующей кристаллической модификации. Если значения D(r)- D _к (r) не укладываются в интервал ошибок ∆ D(r ) кривой D(r ), то для модификации, для которой это расхождение минимально, производится уточнение методом последовательных приближений значений σ_ij с одновременным расчетом N_ij МНК. По получаемому набору N_ij и заданным r_ij и σ_ij каждый раз рассчитывается кривая D ^мнк (r) . Расчет повторяется до тех пор, пока D(r) и D ^мнк (r) не совпадут с точностью до ± ∆ D(r ) . Последнее служит критерием достоверности соответствующего набора N_ij, r_ij и σ_ij . Область подгонки D(r) и D ^мнк (r) ограничивается значениями r_min и r_max, r_min соответствует началу первого максимума, r_max - значению r_ij для последней координационной сферы, для которой N_ij рассчитывается МНК координационное число.

Таким образом, при расчете характеристик ближнего порядка из экспериментальной кривых распределения D(r) МНК для нахождения координационных чисел используется в сочетании с методом последовательных приближений для определения радиусов и размытий координационных сфер. Использование при этом метода размывания кристаллической решетки позволяет смоделировать характер пространственного распределения атомов и оценить степень сооответствия ближнего порядка в исследуемом материале расположению атомовв той или иной кристаллической модификации.

Данная методика позволяет достаточно точно корректно оценить погриешность в значениях N_ij, r_ij и σ _ij , обусловленную случайными ошибками в экспериментальных данных. Для проведения соответствующего анализа запишем систему условных уравнений, используемых для нахождения N_ij МНК в матричной форме.

- матрица-столбец экспериментальных данных, В данном случае это D( r ), рассчитанных по формуле (2.76) ;

- матрица-столбец искомых координационных чисел N_i;

- матрица,элементы которой X_il рассчитываются по формуле :

Индекс l изменяется от 1 до n₁, n₁ – число точек на кривой D(r), j можно опустить, так как число сфер определяется индексом i, а для учета типа взаимодействующих атомов используется признак сорта.

Решение системы условных уравнений в этом случае имеет вид :

Здесь - транспонированная матрица , - матрица, обратная матрице .

Среднеквадратичная ошибка, с которой найдены координационные числа ∆ N_i , определяются через среднеквадратичную ошибку исходных данных dD.

где - диагональный элемент матрицы .

Окончательно ∆ N_i=t_n∆N_i;

t_n - коэффициент Стьюдента для заданной надежности и числа экспериментальных кривых D(r), равного n . Величина dD находится следующим образом: D(r ), из которой производится расчет, должна представлять собой среднюю кривую:

Каждая кривая D_m(r ) рассчитывается из соответствующей экспериментальной зависимости . Таким образом, n - число экспериментальных кривых распределения интенсивности рассеяния.

Среднеквадратичное отклонение ∆ D’(r) в каждой точке r

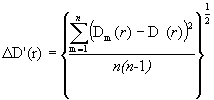
Отсюда

Соответствующие ошибки в значениях r_ij и s _ij можно оценить как интервалы ∆r_ij и ∆ s _ij , изменения в пределах которых не приводят к выходу разности D(r)- D _мнк (r) за пределы экспериментальной ошибки ∆ D(r)=t_n - ∆D’(r) . При этом значения N _ij также остаются в интервале ∆N _ij.

Назад.

Содержание Главы 2.

Содержание Главы 3.

Содержание.