Рентгеноструктурный анализ аморфных материалов
1.2. Вид функции W(r) для кристаллов, газов, жидкостей и аморфных тел
Газы. Пусть частицы, образующие газ, несжимаемы и имеют шарообразную форму. Радиус частицы равен Ro . В силу непроницаемости и несжимаемости частиц можно утверждать, что вероятность их сближения на расстояния, меньшие 2 Ro , равна 0.
В газах, находящихся при нормальном давлении, за пределами r= 2R расположение частиц по отношению к частице, находящейся в начале координат, будет хаотическим, т.е. W(r) = 1 (рис. 2а).
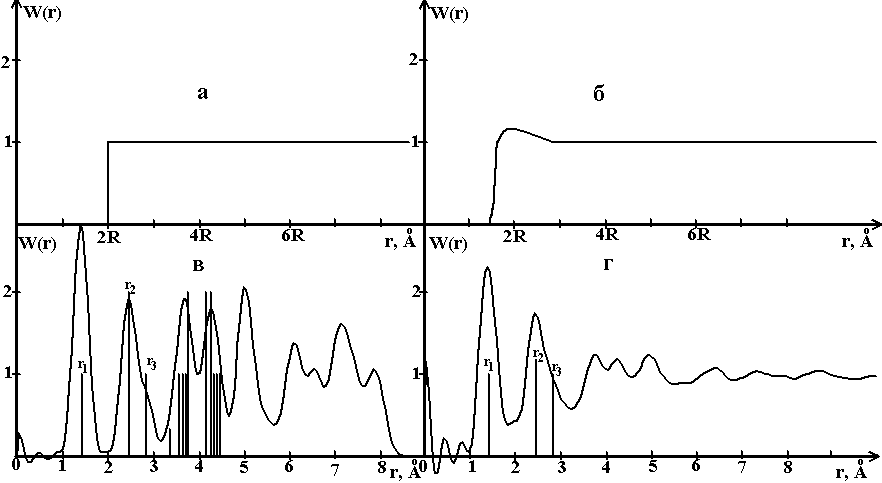
Рис. 2. Функция W(r) [5]:
a, б - для газов (схема), в - расчет для гексагонального графита (48 координационных сфер, размытие 0.1Å); штрихами показаны радиусы первых 13 сфер, высота штрихов ⅓ координационного числа; г - экспериментальная кривая для нанопористого углерода, полученного из карбида кремния.
Кристаллы. В кристаллах функция W(r) не будет зависеть от направления вектора только в том случае, если представить себе, что кристалл вращается вокруг какого-либо фиксированного центра во всех направлениях. (Практически такая ситуация имеет место в кристаллических порошках, при прессовке образца из которых не возникает текстура.) Если считать, что кристалл идеальный и теплового движения образующих его частиц нет, то частицы в нем расположены на фиксированных расстояниях от центральной точки и при вращении их центры будут располагаться строго на сферах радиусов ri , где i = 1,2 ... Такие сферы называются координационными, а число частиц на них Ni - координационным числом. В описанной выше ситуации между сферами центров частиц не будет, то есть dp(r ≠ ri) = 0.
Как следствие, W(r) будет дискретна.
 , (1.13)
, (1.13)
Где δ(r-ri)- дельта-функция Дирака;
 , (1.14)
, (1.14)
Тепловое движение приводит к размытию координационных сфер в кристалле: цен-тры атомов лежат в пределах сферического слоя толщиной ΔR. Последняя определяется величиной амплитуды тепловых колебаний атомов. Дельта-функции в этом случае заме-няются гауссовыми пиками, высота которых определяется значением координационного числа Ni для соответствующей сферы. На рис. 2 в показан результат расчета функции W(r) для гексагонального графита по кристаллографическим данным работы [15n]. Штрихдиа-гамма указывает значения радиусов первых 13 сфер, высота штрихов соответствует ⅓ координационного числа. При полуширине гауссиана, равной 0.1 Å, кривая W(r) непрерывна.
Аморфные твердые тела и жидкости
На рис. 2 г приведена экспериментальная кривая W(r) рассчитанная из рентгенографических данных для аморфного нанопористого углерода, полученного из карбида крем-ния [16n]. Первые два максимума кривой W(r) по форме и соотношению высот соответствуют таковым для гексагонального графита (рис. 2 в). Положения максимумов и пере-гиба на втором максимуме отвечают расстояниям между атомами углерода в пределах кольца (рис. 3 а). Последующие максимумы резко уменьшаются по интенствности и к значению r~10Å осцилляции кривой W(r) аморфного углерода практически затухают.
Таким образом, в аморфных материалах и жидкостях существуют локальные конфигурации, в которых группы атомов сохраняют более или менее определенный характер связи. Если в такой структуре зафиксировать какой-либо атом, то вместо того, чтобы ле-жать на поверхности координационных сфер (рис. 3 а), центры атомов будут находиться в пределах сферических слоев (рис. 3 б), толщина которых dr будет определяться как амплитудами тепловых колебаний, так и разбросом межатомных расстояний относительно их средних значений. Такие локальные конфигурации можно построить около каждого атома системы, и характер взаимного расположения атомов в них не подчиняется ника-ким законам, кроме вероятностных.
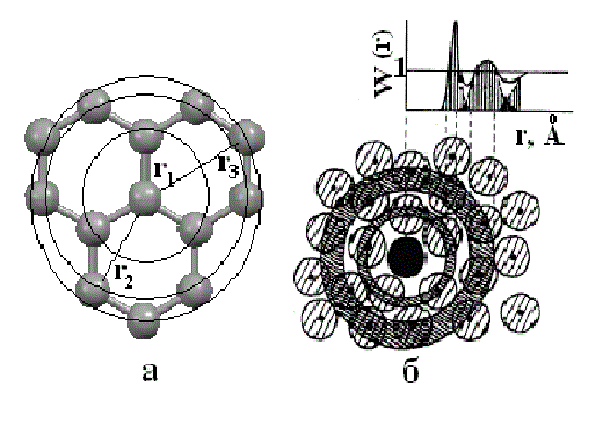
Рис. 3. Первые три координационные сферы в графеновой сетке (а); сферические слои в неупорядоченной конфигурации и соответствующая им кривая W(r)
Функция радиального распределения осциллирует около 1, ее максимумы соответ-ствуют наиболее вероятным межатомным расстояниям, а минимумы – расстояниям, на которых центры атомов находятся редко. По мере увеличения r любые расстояния между атомами становятся равновероятными, то есть W(r)→1. Значение r, при котором функция радиального распределения атомов становится равной 1, определяет размеры области ближнего упорядочения, то есть дальность корреляции в расположении атомов.
Таким образом, положения пиков на кривой радиального распределения атомов W(r) соответствуют значениям радиусов координационных сфер rij, а их размытия σij ха-рактеризуют дисперсию межатомных расстояний. Дальность корреляции определяется значением r, дальше которого функция радиального распределения W(r) практически не отличается от 1. Координационные числа Nij рассчитываются из площадей под максиму-мами функций радиального распределения атомной и электронной плотностей: p(r) и pе(r) соответственно.
Все указанные характеристики дают информацию о структуре аморфного матери-ала. Основными методами получения функций радиального распределения атомов W(r), атомной p(r) и электронной pе(r) плотностей являются дифракционные методы: рентгено-, электроно- и нейтронография. Современные методы расчета позволяют корректно рас-считать значения координационных чисел Nij вплоть до 10 - 15 координационных сфер.