Цель работы:

Из рентгенографического эксперимента (зависимость интенсивности рассеяния от угла рассеяния, рентгенограмма), выполненного на кристаллических порошковых материалах определить структурные характеристики и, в частности, коэффициенты заполнения атомных позиций и оценить погрешности данных величин.

Задание для студента:

1. Главным условием рентгеновского эксперимента является получение дифракционной картины, погрешность измерения интенсивности рассеяния рентгеновских лучей образцом в каждой точке которой не выше 5%. Это достигается путем многократной регистрации дифракционной картины и усреднением данных в каждой ее точке.
   Рассчитайте погрешность в j-й точке как среднеквадратичное отклонение ΔI_i² по формуле: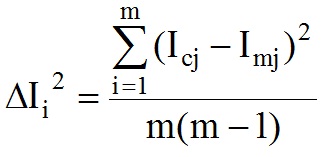
   Здесь I_cj и I_mj среднее значение интенсивности (рассчитанное и экспериментальное соответственно) и значение ее на каждой i-й кривой в j-й точке. m – число зарегистрированных кривых.
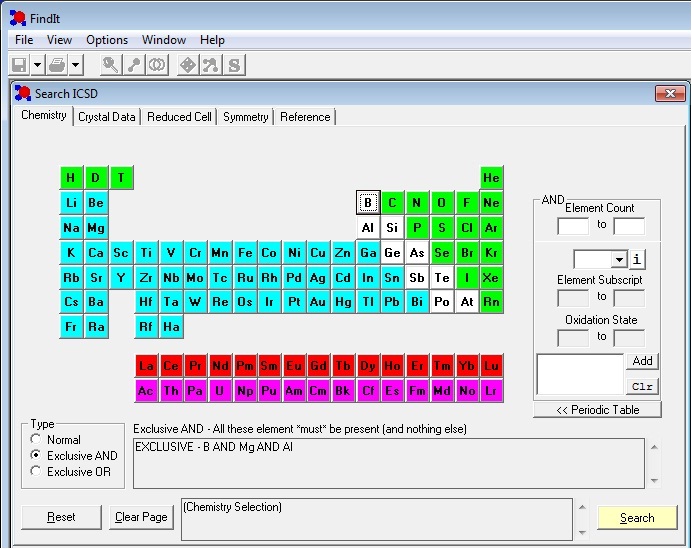
2. Далее в базе данных ICSD выберите соединения, в состав которых входят элементы, составляющие соединение: Al, Mg, B, как показано на рисунке 1: Рис 1. Выбор элементов для поиска соединений в базе данных ICSD с помощью программы FindIt.
   На рисунке 2 представлен результат поиска соединений системы Аl_xMn_yB_z в базе данных ICSD. Всего найдено 13 соединений различного состава.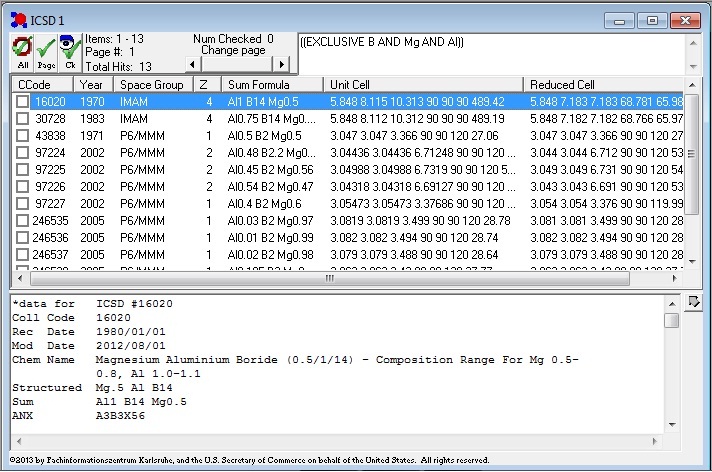 Рис. 2 . Результат поиска соединений системы Аl_xMn_yB_z в базе данных ICSD
   
3. Рассчитайте в программе FindIt дифракционную картину для кристаллических модификаций и сравните ее с экспериментальной.
   Если рассчитанная и экспериментальная рентгенограммы не совпадают по положениям отражений, то значит ни состав, ни расположение атомов в элементарной ячейке не соответствуют исследуемому соединению.
4. Обработайте экспериментальную рентгенограмму методом полнопрофильного анализа и уточнените профильные и структурные характеристики.
   Расчет проводится нелинейным методом наименьших квадратов, то есть система уравнений составляется относительно приращений заданных исходных значений этих величин. К минимуму сводится функционал вида: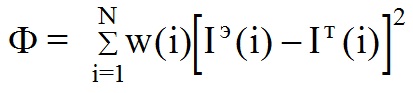 где:
   I^э(i), I^т(i) - полученные экспериментально для исследуемого образца и рассчитанные для модели структуры кристалла интенсивности рассеяния в i-й точке профиля рентгенограммы
   w(i) - весовая функция
   N - число точек профиля
   

Степень совпадения экспериментального и подобранного в процессе уточнения теоретического профилей рентгенограмм оценивается по значению стандартного фактора недостоверности R:

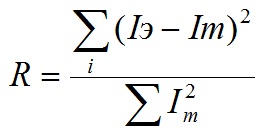
Ошибки в координатах атомов и коэффициентах заполнения позиций рассчитываются в процессе расчета приращений методом наименьших квадратов.

Метод уточнения профильных и структурных параметров

Поскольку функция I^т(i) , описывающая теоретическую рентгенограмму, нелинейно зависит как от параметров модели кристалла, которые надо уточнить, так и от профильных параметров, то в формуле она заменяется на два первых слагаемых в разложении ее в ряд Тейлора: 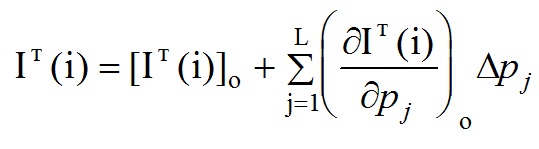Через pj обозначены уточняемые параметры, а через Δpj - их приращения. Число уточняемых параметров обозначено через L. На начальном этапе расчета интенсивности в каждой точке профиля рентгенограммы [I^т(i)]_o и первые производные 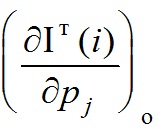рассчитываются для начальных значений уточняемых параметров pj.

Условие минимума функционала Ф по l-му параметру имеет вид:

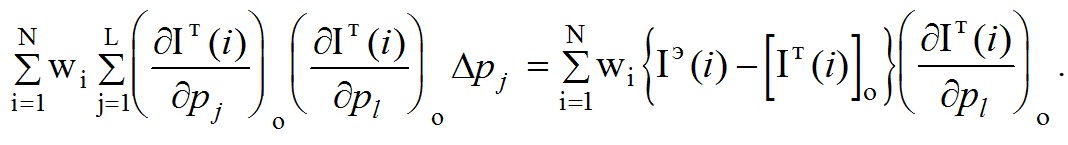
Уравнения данного типа, записанные для каждого из L уточняемых параметров модели, образуют систему из L уравнений, линейных относительно L приращений Δpj, которая может быть решена методом Гаусса или матричным способом.

В матричной форме эта система записывается как: [A]×[Δpj]=[B],

где jl-е элементы матриц [А] (А_jl) и [В] (B_j) равны соответственно

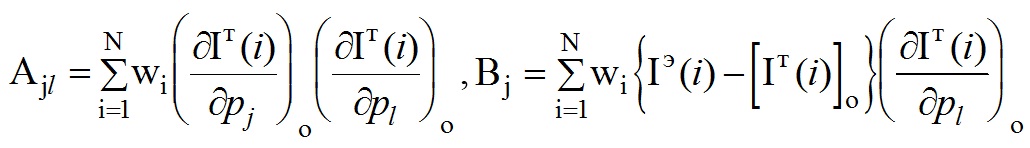
Решение уравнения будет иметь вид: [Δpj] = [A]^-1×[B],

где [A]^-1 - матрица, обратная матрице [A].

Уточненные параметры pj= pj+Δpj используются для нового расчета теоретической рентгенограммы, функционала и факторов недостоверности.

Назад