На главную страницу

Назад                                                                                                                    Вперед

Дифференциальное сопротивление эмиттерного и коллекторного перехода

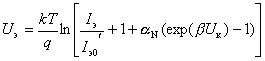
Из  ВАХ биполярного транзистора

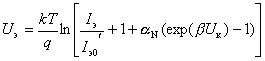
 легко получить общее выражение для дифференциального сопротивления эмиттерного перехода:

,                              

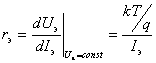Для примера рассчитаем r_э при I_э = мА, получим – r_э = 25 Ом.

Если U_э= 0 (условие короткого замыкания), тогда .

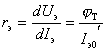Если I_э = 0 (условие холостого хода), то .

Дифференциальное сопротивление коллекторного перехода r_к определяется как

.

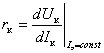 В активном режиме при U_к << 0 зависимость тока коллектора I_к от параметров биполярного транзистора выглядит следующим образом: I_к = aI_э + I_к0. Из приведенного соотношения следует, что в явном виде ток коллектора I_к от напряжения на коллекторе U_к не зависит. Поэтому в первом приближении сопротивление коллекторного перехода r_к при U_к << 0 стремится к бесконечности.

 Проанализируем возможность зависимости коэффициента передачи a от напряжения на коллекторе U_к. Эта зависимость может проявиться через следующие цепочки: изменение напряжения на коллекторе изменит ширину объединенной области p-n перехода, в свою очередь изменение ширины объединенной области p-n перехода вызовет изменение ширины базы, а изменение ширины базы изменит коэффициент передачи эмиттерного тока. С учетом изложенного получим следующие выражения для расчета дифференциального сопротивления коллекторного перехода:

Изменение коэффициента передачи a биполярного транзистора вследствие модуляции ширины базы при изменении коллекторного напряжения U_к получило название “эффект Эрли” (рис. 7).

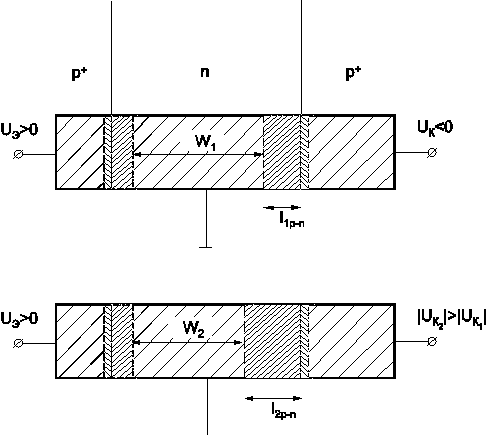
Рис. 7. Эффект Эрли – эффект модуляции ширины базы биполярного транзистора

Рассмотрим, как модуляция ширины базы влияет на коэффициент передачи a. Выражение для коэффициента передачи a имеет следующий вид:

.

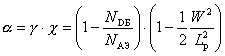Для нессимметричного p⁺-n перехода обедненная область локализована в слабо легированной части p-n перехода и ее ширина .

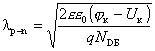При изменении напряжения на коллекторе U_к меняется ширина обедненной области , а следовательно, и ширина базы биполярного транзистора W. Этот эффект обуславливает конечное значение дифференциального сопротивления коллекторного перехода. Более подробно соотношение (5.23) перепишем в следующем виде:

.                                 

С учетом сказанного получаем выражение для дифференциального сопротивления коллекторного перехода:

.                                     

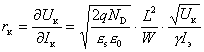Рассчитаем для примера численное значение сопротивления коллекторного перехода r_к при следующих параметрах биполярного транзистора на основе кремния (Si):

N_D = 10¹⁵ см^-3; L = 0,1 мм; W = 30 мкм, U_к = 5В, I_э = 1 мА, e_Si = 11,8.

Подставляя параметры , получаем r_к » 5,2 МОм.

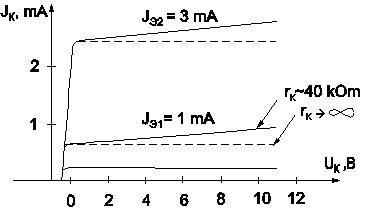
Рис. 8. Коллекторные характеристики биполярного транзистора в схеме с общей базой,

иллюстрирующие влияние эффекта Эрли

5.10. Коэффициент обратной связи

Коэффициент обратной связи по напряжению в биполярном транзисторе в схеме с общей базой показывает, как изменится напряжение на эмиттерном переходе при единичном изменении напряжения на коллекторном переходе при условии, что ток эмиттера поддерживается постоянным:

.

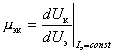Ненулевое значение коэффициента обратной связи также обусловлено эффектом Эрли. Аналогично, как и для коллекторного напряжения, распишем цепочку, показывающую взаимосвязь параметров.

Требование постоянства эмиттерного тока I_э = const для биполярного транзистора при диффузионном механизме переноса носителей через базу обуславливает постоянство градиента концентрации инжектированных носителей . При увеличении напряжения на коллекторе U_к увеличивается ширина обедненной области  коллекторного p-n перехода, что вызывает уменьшение ширины квазинейтрального объема базы W. Это, в свою очередь, влечет за собой уменьшение концентрации инжектированных носителей р_n(0) на границе эмиттерного перехода (так как градиент  должен оставаться постоянным). Поскольку концентрация инжектированных дырок на границе эмиттерного перехода р_n(0)= p­₀·exp(bU_э) определяется напряжением на эмиттере, то ее уменьшение возможно только при уменьшении напряжения U_э на эмиттере.

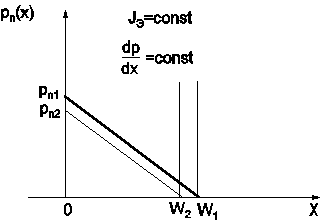
Рис. 9. Влияние эффекта модуляции ширины базы БТ на

концентрацию неосновных носителей на границе эмиттер–база

Таким образом, если поставлено условие: I_э = const, , то при увеличении коллекторного напряжения U_к должно происходить уменьшение эмиттерного напряжения U_э.

Физически наличие обратной связи по напряжению в биполярном транзисторе в схеме с общей базой обусловлено эффектом модуляции ширины базы.

Получим выражение для коэффициента обратной связи. Поскольку , то . Учтем, что, так как градиент постоянен. Зависимость ширины базы от напряжения на коллекторе  была получена ранее. Тогда

.

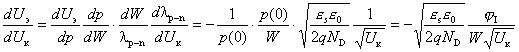Таким образом, выражение для коэффициента обратной связи по напряжению m_эк в биполярном транзисторе в схеме с общей базой в зависимости от конструктивно-технологических параметров имеет следующий вид:

.                                          

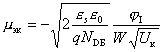Подставив те же параметры биполярного транзистора те же, что и в предыдущем примере, получаем m_эк = –1,1 10^-5. Знак “–” в выражении для m_эк означает, что при увеличении напряжения на коллекторе U_к происходит уменьшение напряжения на эмиттере U_э.

На главную страницу